Kezdőlap


Feladat:	1960. évi Matematika OKTV II. forduló 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1960/november, 102 - 104. oldal		PDF \| MathML
Témakör(ök):	Súlyvonal, Trapézok, OKTV
Hivatkozás(ok):	Feladatok: 1960/szeptember: 1960. évi Matematika OKTV II. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Húzzuk meg a négyszög $A C$ és $B D$ átlóit. Az $A F$ és $C E$ szakasz az $A C D$ , ill. $A B C$ háromszögben súlyvonal, tehát a háromszöget két egyenlő területű háromszögre osztja (8. ábra):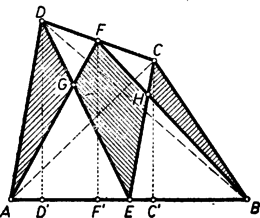

8. ábra

\begin{matrix} A D F = A C F, B C E = A C E \end{matrix}

(1)

(az idomok területét ugyanúgy jelöljük, mint magukat az idomokat). Ezekből összeadással

\begin{matrix} A D F + B C E = A E C F, \end{matrix}

(2)

mert az

A B C D

négyszög konvexsége folytán

D

és

B

A C

-nek ellentétes partján feküsznek, és ezért ugyanez áll

F

és

E

-re is. Figyelembe véve a

D E

és

B F

egyenesekkel való felbontást is, (2)-t így írhatjuk:

\begin{matrix} A D G + D G F + B C H + B H E = A E G + C F H + E H F G \end{matrix}

(3)

(mindkét oldalon az

A B C D

négyszög területének fele áll).
Hasonlóan a

D E

és

B F

súlyvonalakkal két-két egyenlő részre osztott

A B D

és

B C D

háromszögekből

\begin{matrix} A D E + B C F = E B F D, \end{matrix}

(4)

amit részletesebben így írhatunk:

\begin{matrix} A D G + A E G + B C H + C F H = B H E + D G F + E H F G . \end{matrix}

(5)

Már most (3) és (5) összegéből a két oldalon fellépő egyenlő tagok elhagyásával és 2-vel való osztással a bizonyítandó egyenlőséget kapjuk:

\begin{matrix} A D G + B C H = E H F G . \end{matrix}

II. megoldás: Ismeretes, hogy a trapézt átlói négy olyan háromszögre bontják, melyek közül a szárakra támaszkodók egyenlő területűek. Ezt a tételt fogjuk háromszor felhasználni. Feltehetjük, hogy

D

és

C

közül

D

van távolabb

A B

-től. Húzzunk

D

-n és

C

-n át

A B

-vel párhuzamost és jelöljük ezeknek

A F

meghosszabbításával, ill.

B F

-fel való metszéspontját

D'

, ill.

C'

-vel (9. ábra), továbbá

E D'

és

F C'

metszéspontját

J

-vel.

9. ábra

A E D' D

és

E B C C'

trapézok, így

\begin{matrix} A G D = E G D' \end{matrix}

és

\begin{matrix} B C H = E H C' . \end{matrix}

E G D'

és

E H C'

háromszögek együttesen nem takarják le az

E H F G

négyszöget, kinyúlik az

F D' J

, nincs lefedve az

E C' J

háromszög. Ha sikerül igazolnunk, hogy ezek egyenlő területűek, akkor a feladat tételét bebizonyítottuk. Ehhez viszont elegendő megmutatni, hogy

C' D'

párhuzamos

E F

-fel, mert ekkor az

E C' D' F

négyszög trapéz voltából következik állításunk.
Jelöljük

C C'

-nek

E F

és

A F

-fel való metszéspontját

P

, ill.

Q

-val. Így

E F

A B

szakasszal együtt a vele párhuzamos

Q C'

szakaszt is felezi. Másrészt a

Q C F

és

D' D F

háromszögek egybevágóságából következik, hogy

Q F = F D'

. Tehát

P

, ill.

F

Q C' D'

háromszög

Q C'

, ill.

Q D'

oldalának felezőpontja, és így valóban

P F

párhuzamos

C' D'

-vel.
Ha

D

és

C

egyenlő távolságra esnek

A B

-től, akkor

D'

és

C'

egybeesnek

F

-fel, és így az

E G D'

és

E H C'

háromszögek együtt pontosan lefedik az

E H F G

négyszöget.

III. megoldás: Azt mutatjuk meg, hogy

\begin{matrix} A E D + E B C = A B F, \end{matrix}

illetőleg e területeket 2, 2, ill. 3 idom területének összegeként felírva

\begin{matrix} A E G + A D G + E B H + B C H = A E G + E B H + E H F G . \end{matrix}

Innen ugyanis a két oldal egyenlő tagjainak elhagyásával a bizonyítandó tételt kapjuk.
Valóban,

D

F

C

-nek

A B

-n levő vetületét rendre

D'

F'

C'

-vel jelölve (8. ábra) a

C D D' C'

idom trapéz, és benne

F F'

a középvonal, tehát

\begin{matrix} \frac{D D'}{2} + \frac{C C'}{2} = F F' . \end{matrix}

Innen pedig mindkét oldalt

A E

-vel szorozva, majd az

A E = E B = A B / 2

egyenlőségeket figyelembe véve

\begin{matrix} \frac{1}{2} A E \cdot D D' + \frac{1}{2} E B \cdot C C' = \frac{1}{2} A B \cdot F F' \end{matrix}

adódik, ami állításunkat igazolja.

Megjegyzések. 1. A feladat állítása általánosítható: a kimondott területegyenlőség akkor is fennáll, ha

E

és

F

A B

, ill.

C D

oldalt (nem felezi, hanem) ugyanolyan

q

arányban osztja két-két részre:

A E : E B = q

, azaz

A E = q \cdot E B

, és ugyanígy

C F = q \cdot F D

(10. ábra, itt

q = 2

10. ábra

Az állítás mindhárom fenti megoldás gondolatmenetével igazolható; alább az I. megoldás módosításával bizonyítjuk. Az ott szereplő (1)‐(3) egyenlőségek jobb oldala most a bal oldal

q

-szorosával lesz egyenlő, (4) és (5) bal oldala viszont a jobb oldal

q

-szorosával. Így a (3) és (5)-ből keletkezett egyenlőségek összegében 2 helyett

(1 + q)

-val osztva kapjuk az általánosítás állítását. Ez az általánosítás Bollobás Béla dolgozatában szerepel.
2. Könnyű belátni, hogy a nem konvex (vagyis az egy

180^{\circ}

-nál nagyobb belső szöggel bíró, valamint a hurkolt) négyszögekre az állítás nem igaz.