Feladat: 1960. évi Matematika OKTV II. forduló 2. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1960/november, 99 - 102. oldal  PDF  |  MathML 
Témakör(ök): Tengelyes tükrözés, Középponti és kerületi szögek, Trapézok, OKTV
Hivatkozás(ok):Feladatok: 1960/szeptember: 1960. évi Matematika OKTV II. forduló 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A feltevések folytán P az F ponthoz tartozó FG átmérővel kettévágott k kör azon félkörének belsejében van, amelynek ívén 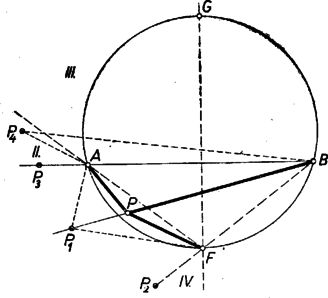A fekszik.
a) Tulajdonképpen csak az AFG szögtartományban fekvő P pontokra kell bizonyítást adnunk, mert az FA húrral lemetszett kisebb körszeletben levő P pontokra az állítás magától értetődő, hiszen ilyenkor A és B az FP egyenes ugyanazon partján vannak, és ezért az FPB szög része az APF szögnek (1. ábra).

 
 
1. ábra
 

Másképpen: ilyen esetekben a PB félegyenes benne van az APF szögtartományban.
b) Ugyanez áll akkor is, ha P az FA húron van, mert ilyenkor az APF szög bármelyik irányú forgással 180∘, az FPB szög pedig kisebb.
c) Ha P az AFG szögtartományban van, akkor FP szétválasztja A-t és B-t. (2. áb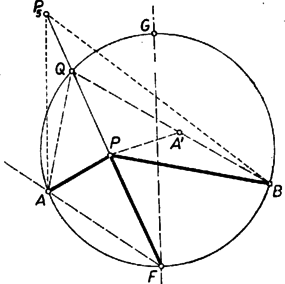ra).
 
 
2. ábra
 

Tükrözzük FP-re az APF szöget, legyen az A pont tükörképe A'. Ekkor elegendő azt igazolnunk, hogy az FPB szög része az FPA-val egyenlő FPA' szögnek. ‐ Messe az FP egyenes k-t másodszor Q-ban. Így egyrészt az FQA és FQB szögek egyenlők, mert k-nak a száraik közti FA, FB ívei egyenlők, másrészt a tükrözés folytán az FQA és FQA' szögek egyenlők, és ezért A' és QB egyenesen van, továbbá QA'=QA<QB, tehát A' a QB húr belső pontja. Így pedig a PB félegyenes valóban az A'PF szögtartományban van.
A fentiekben az állítást P minden lehetséges helyzetére igazoltuk.
 

Megjegyzések. 1. Nem használtuk fel, hogy az F-fel felezett AB ív kisebb félkörnél, ezért az állítás bármekkora AB ívre érvényes.
2. A bizonyítás a) részében nem használtuk fel, hogy P a k-n belül van, így meggondolásunk az ABF szögtartomány k-n és rajta kívül fekvő I. része minden pontjára érvényes (az 1. ábrán P1), úgyszintén a BF szakasz F-en túli meghosszabbításának P2 pontjaira is, mert így a P2B és P2F félegyenesek egybeesnek, szögük 0. Az I. síkrész másik határoló félegyenesén, a BA szakasz A-n túli meghosszabbításán levő P3 pontokra viszont a két kérdéses szög azonos.
Kézenfekvő most már legalább vázlatosan áttekinteni a kérdéses szögek nagyságviszonyát minden az (1)-et teljesítő P pontra. Ha P kilép I-ből BA-nak A-n túli meghosszabbításán át, de nem lépi át FA-t (II. síkrész, P4), akkor a PB félegyenes kilép az APF szögtartományból, APF része BPF-nek, (2) iránya ellentétesre fordul. Ugyanez adódik a III. síkrészben, vagyis ha P az AFG szögtartománynak k-n kívüli pontja (a 2. ábrán P5), mert ilyenkor a c) alatti Q pont F és P5 közé esik, és így 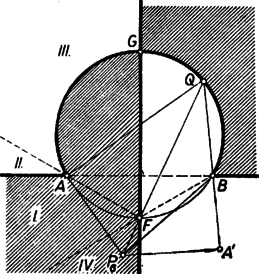A'P5F∢<BP5F∢.
 
 
3. ábra
 

Végül a IV. síkrészben választott P6-tal Q a GB íven adódik (3. ábra), ezért QA'>QB, így AP6F∢=A'P6F∢>BP6F∢, itt tehát érvényes (2). ‐ Most már a PA>PB követelmény mellett a megfelelő síkrészek határvonalait FG-re tükrözéssel kapjuk, így a 3. ábra csíkozott részein a kérdéses szögek közül APF nagyobb, a világosakon FPB nagyobb, a határvonalakon pedig a két szög ‐ amint az könnyen belátható ‐ egyenlő. (Mezei Ferenc ,,térképvázlata'').
A további megoldásokban csak a fenti c) esettel foglalkozunk, ezt 3 alesetre bontjuk fel aszerint, hogy P az AB-nek F-fel ellentétes, ill. megegyező partján van ‐ vagyis az utóbbi alesetben az ABF háromszögben ‐ vagy pedig magán az AB húron. ‐ Mindkét további megoldás Muszély György megoldásainak egyszerűsítése.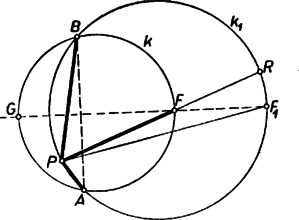
 
 
4. ábra
 

II. megoldás: c1) Ha P az AB-nek F-fel ellentétes oldalán van (4. ábra), akkor a kérdéses APF és FPB szögek a kisebb APB szögnek részei. Az A, B, P pontokon átmenő k1 kör P-t nem tartalmazó, vagyis k-n kívül levő AB ívének F1 felezőpontja az AB egyenesnek F-fel egyező oldalára, vagyis GF-nek F-en túl való meghosszabbítására esik. Így F1 az APF szögtartományban van, F pedig az F1PB szögtartományban. Ámde PF1 felezi a kisebb APB szöget, ennélfogva az APF szög F1PF szöggel nagyobb, az FPB szög pedig ugyanennyivel kisebb az APB szög felénél, ez megfelel az állításnak.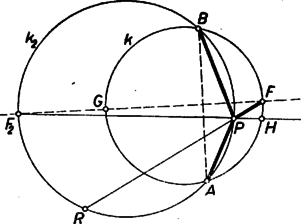
 
 
5. ábra
 

c2) Ha P az AB-nek F-fel egyező oldalán van (5. ábra), akkor az A, B, P pontokon átmenő k2 kör P-t nem tartalmazó, vagyis k-n kívül levő AB ívének F2 felezőpontja az AB egyenesnek F-fel ellentétes oldalára, FG-nek G-n túl való meghosszabbítására esik. A kérdéses APF és FPB szögek egyenes szögnél nagyobb összegét ebben az alesetben F2P-nek P-n túl való PH meghosszabbítása felezi. A PH félegyenes FG-nek A-t tartalmazó oldalán van, ezért az APF szöget osztja részekre. Így az APF szög nagyobb, FPB pedig kisebb az APH=HPB szögnél. Ezt kellett bizonyítanunk.
c3) Végül ha P az AB szakaszon van, akkor (2) fennáll, mert APF tompaszög, FPB pedig hegyesszög.
 

Megjegyzések. 1. A c2) aleset meggondolása nem alkalmazható az FA húrral lemetszett körszeletben felvett P-re, mert ilyen esetben a 180∘-nál nagyobb APF szöget hasonlítanók az FPB szöghöz.
2. Lényegében a fenti meggondolást mondjuk el másképpen annak az R pontnak a helyzetét tekintetbe véve, ahol a PF egyenes a k1, ill. k2 kört másodszor metszi.
A c1) alesetben (4. ábra) F a k1-re nézve belső pont, ezért R egyrészt a PF szakasz F-en túl való meghosszabbításán van, FG-nek P-vel ellentétes, vagyis B-vel egyező oldalán. Másrészt R a P-t nem tartalmazó AB ívnek pontja. Ezek szerint R a (rövidebb) BF1 íven van. Így k1-nek AF1R íve hosszabb a BR ívnél, tehát APR∢>RPB∢, vagyis APF∢>FPB∢.
A c2) alesetben (5. ábra) F a k2-re nézve külső pont, ezért R egyrészt az FP szakasz P-n túli meghosszabbításán van, FG-nek P-vel egyező, B-vel ellentétes oldalán, másrészt az AF2B íven. Így R a (rövidebb) AF2 ívnek pontja, AR^< <RB^, APR∢<RPB∢, ezért 180∘-APR∢>180∘-RPB∢, azaz APF∢>FPB∢.
 

III. megoldás: A feladat állítása akkor és csak akkor igaz, ha az APF háromszög A és F-nél levő (belső) szögeinek összege kisebb, mint a BPF háromszög B és F-nél levő (belső) szögeinek összege. Ezt fogjuk bizonyítani.
Legyen P tükörképe FG-re P', így az APP'B négyszög konvex trapéz.
A c1) alesetben P' az FBP szögtartományban van (6. ábra).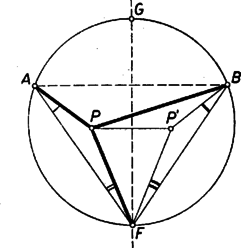
 
 
6. ábra
 

Ugyanis P és P' az ABP háromszög belsejében vannak, tehát P'BA∢<FBA∢, másrészt az ABP háromszögből (1) alapján PBA∢<PAB∢=P'BA∢. Ennélfogva
 

PAF∢=P'BF∢<PBF∢.(3)
Másrészt P' a BFG szögtartományban van, amely része BFP-nek, ezért
PFA∢=P'FB∢<PFB∢.(4)
Most már (3) és (4) két-két szélső tagjának összeadásával a kívánt egyenlőtlenség adódik.
 
 
7. ábra
 

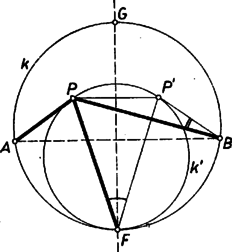Ha pedig AB elválasztja P-t és F-et (7. ábra), akkor egyrészt
PFB∢-PFA∢=PFB∢-P'FB∢=PFP'∢,(5)
ez pedig PP' látószöge F-ből; másrészt
PAF∢-PBF∢=P'BF∢-PBF∢=PBP'∢,(6)
ez pedig PP' látószöge B-ből; ekkor B ugyanazon oldalán fekszik PP'-nek, mint F. ‐ Mármost a PP'F háromszög köré írt k' kör érinti k-t F-ben, minden más pontja k belsejében van, így B a k'-re nézve külső pont. Ezért PP'-nek B-ből vett látószöge kisebb az F-ből vett látószögénél, azaz (5) és (6) alapján
PAF∢-PBF∢<PFB∢-PFA∢.
Innen pedig átrendezéssel
PAF∢+PFA∢<PBF∢+PFB∢,
amit bizonyítani akartunk.