Kezdőlap


Feladat:	1960. évi Matematika OKTV I. forduló 3. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1960/szeptember, 14 - 16. oldal		PDF \| MathML
Témakör(ök):	Egyenlő szárú háromszögek geometriája, Középpontos és egyéb hasonlósági transzformációk, Háromszögek hasonlósága, Teljes indukció módszere, OKTV
Hivatkozás(ok):	Feladatok: 1960/szeptember: 1960. évi Matematika OKTV I. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a $B A C$ szög nagysága $φ$ , így az $A B C$ szög $n φ$ . Ezek különbözők, ezért a háromszög szárai vagy $A$ -ban, vagy $B$ -ben futnak össze. Az állítást a két esetre külön-külön bizonyítjuk.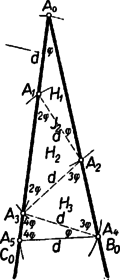
I. eset: a szárak $A B$ és $A C$ , tehát a $C$ csúcsnál levő szög nagysága $n φ$ , a szögek összegéből $φ = 180^{\circ} / (2 n + 1)$ , ez hegyesszög, mert $2 n + 1 \geq 5$ , és $n φ$ ugyancsak hegyesszög. ‐ Elegendő egy olyan $A_{0} B_{0} C_{0}$ háromszöget adnunk, amely $n - 1$ egyenes vágással $n$ egyenlő szárú háromszögre bontható egyenlő hosszú szárakkal és hasonló az $A B C$ háromszöghöz. Nyilvánvaló ugyanis, hogy az $A_{0} B_{0} C_{0}$ -t $A B C$ -be átvivő hasonlósági transzformációval valamennyi vágásszakasz megfelelőjét $A B C$ -ben megszerkesztve és e háromszöget a kapott szakaszok mentén szétdarabolva ebből is $n$ egyenlő szárú háromszög áll elő egyenlő hosszú szárakkal.
Egy a kívánt tulajdonsággal bíró $A_{0} B_{0} C_{0}$ háromszöget egy $A_{0}$ csúcsú, $φ$ nagyságú szögből kiindulva a következő, $n + 1$ lépésből álló és lépésenként 1‐1 újabb segédpontot előállító szerkesztéssorozattal kaphatunk. A segédpontokat rendre $A_{1}, A_{2}, ..., A_{n}, A_{n + 1}$ -gyel jelöljük. Első lépésül $A_{0}$ -ból egy tetszés szerinti $A_{0} A_{1} = d$ szakaszt mérünk a szög egyik szárára (1. ábra, ezen $n = 4$ ).

1. ábra

A 2. lépésben

A_{1}

körül

d

sugárral kört írva

A_{2}

-ként vesszük e körnek a szög másik szárán levő,

A_{0}

-tól különböző metszéspontját. A további pontokat váltakozva a szög egyik és másik szárából metsszük ki az utoljára kapott pont körül

d

sugárral írt körívvel és mindig úgy, hogy azok a korábbi metszéspontoktól különbözők legyenek. Így

A_{3}

gyanánt az

A_{2}

körül

d

sugárral írt körnek a szög első,

A_{0} A_{1}

szárán levő,

A_{1}

-től különböző metszéspontját vesszük. Az

n + 1

-edik lépés után

A_{n}

-t

B_{0}

-nak,

A_{n + 1}

-et

C_{0}

-nak véve előttünk áll a kívánt

A_{0} B_{0} C_{0}

háromszög, és ezt az

A_{1}

-től

A_{n}

-ig terjedő egymás utáni

n - 1

segédpontpárt összekötő

n - 1

egyenlő szakasz darabolja fel a kívánt módon.
Mivel az

A_{0}

-nál levő

φ

szög hegyesszög, azért

A_{2}

valóban a másik száron jön létre. Az

A_{1} A_{0} A_{2} = H_{1}

háromszög egyenlő szárú, így

A_{2}

-nél levő szöge is

φ

, tehát

A_{1}

-nél levő külső szöge

φ + φ = 2 φ

. ‐ Ez is hegyesszög, ezért

A_{3}

A_{0}

-tól távolabb jön létre, mint

A_{1}

. Így az említett külső szög az

A_{2} A_{1} A_{3} = H_{2}

egyenlőszárú háromszögnek belső szöge, tehát

H_{2}

-nek

A_{3}

-nál levő szöge is

2 φ

, továbbá

H_{2}

kívül áll

H_{1}

-en,

A_{1} A_{2}

oldaluk közös,

A_{1}

-be befutó

A_{1} A_{3}

és

A_{1} A_{0}

oldalaik egymás meghosszabbításai, így együtt kitöltik az

A_{0} A_{2} A_{3} = J_{2}

háromszöget. Ezért az

A_{1} A_{3} A_{2}

szög

J_{2}

-nek is szöge, ennélfogva

J_{2}

-nek

A_{2}

-nél levő külső szöge

φ + 2 φ = 3 φ

. ‐ Ha

n > 2

, vagyis

n \geq 3

, akkor

3 φ

is hegyesszög, így

A_{4}

távolabb van

A_{0}

-tól, mint

A_{2}

. Ezért az

A_{3} A_{2} A_{4} = H_{3}

egyenlő szárú háromszög kívülről csatlakozik

J_{2}

-höz és

A_{4}

-nél levő szöge is

3 φ

, egyenlő az utóbbi külső szöggel. Az

A_{3} A_{4} A_{2}

szög a

J_{2}

és

H_{3}

-ból összetevődő

A_{0} A_{3} A_{4} = J_{3}

háromszögnek is szöge, így

J_{3}

-nak

A_{3}

-nál levő külső szöge

φ + 3 φ = 4 φ

.
Teljes indukcióval minden

k \leq n

-re könnyű belátni, hogy az

A_{k} A_{k - 1} A_{k + 1} =

= H_{k}

egyenlő szárú háromszögben

A_{k} A_{k - 1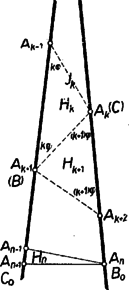} A_{k + 1} ∢ = A_{k} A_{k + 1} A_{k - 1} ∢ = k φ

(2. ábra).

2. ábra

Ennek helyességét

k = 1, 2

-re és

n \geq 3

mellett

k = 3

-ra az előzőkben láttuk. Ha már most

k

olyan az

n

-nél kisebb szám, amelyre állításunk érvényes, akkor érvényes

k + 1

-re is. Ugyanis

k < n

folytán

k + 1 \leq n

, és így a műveletsorozat még folytatódik. Az

A_{0} A_{k} A_{k + 1} = J_{k}

háromszög

A_{k}

-nál levő külső szöge

(k + 1) φ \leq n φ < 90^{\circ}

, ezért az

A_{k + 1}

körüli

d

sugarú körrel az

A_{0} A_{k}

szárból kimetszett

A_{k + 2}

távolabb van

A_{0}

-tól, mint

A_{k}

, tehát az

A_{k + 1} A_{k} A_{k + 2} = H_{k + 1}

egyenlő szárú háromszög kívülről csatlakozik

J_{k}

-hoz. Így

J_{k}

-nak

A_{k}

-nál levő

(k + 1) φ

nagyságú külső szöge

H_{k + 1}

-nek belső szöge, tehát

A_{k} A_{k + 2} A_{k + 1} ∢ = A_{k + 2} A_{k} A_{k + 1} ∢ = (k + 1) φ

. Ezek szerint állításunk érvényessége valóban öröklődik minden az

n

-nél kisebb

k

-ról

k + 1

-re.
Tekintsük most már a

J_{n} = A_{0} A_{n} A_{n + 1} = A_{0} B_{0} C_{0}

háromszöget. Ebben a fentiek szerint

A_{0} C_{0} B_{0} ∢ = A_{0} A_{n + 1} A_{n} ∢ = A_{n - 1} A_{n + 1} A_{n} ∢ = n φ

, és ezért

A_{0} B_{0} C_{0} ∢ = 180^{\circ} - φ - n φ = (2 n + 1) φ - (1 + n) φ = n φ

. Így

J_{n}

egyenlő szárú, a szögek egyenlősége folytán hasonló az adott

A B C

háromszöghöz és maradéktalanul szétvágható a

H_{1}, H_{2}, ..., H_{n}

egyenlő szárú háromszögekre. A szerkesztéssorozat első és utolsó lépése, az

A_{0} A_{1}

és

A_{n} A_{n + 1}

szakasz nem vágandó, tehát a vágások száma

(n + 1) - 2 = n - 1

. Mindezek szerint

J_{n}

-nek megvan a kívánt tulajdonsága. Ezt kellett megmutatnunk.
Továbbhaladás előtt vegyük észre, hogy az

A_{0} B_{0} C_{0}

háromszögben

B_{0} C_{0} = A_{n} A_{n + 1} = d

. Ennek alapján megtakaríthatjuk a hasonlósági transzformációt: a fenti szerkesztéssorozatot az adott háromszögben

A

-ból kezdve és

d = B C

-vel végrehajtva azonnal a kívánt felbontást kapjuk. Így

A_{n}

és

A_{n + 1}

kitűzése elmarad. A szerkesztéssorozatot fordított sorrendben, azaz

B

vagy

C

-ből kezdve is végrehajthatjuk, ilyenkor

A_{n - 1}

az első szerkesztett pont.
Vegyük észre azt is, hogy szerkesztéssorozatunk első

k + 1

lépésével, ill. az

A_{1} A_{2} ... A_{k - 1} A_{k}

vágássorozat

k - 1

vágásával, az

A_{0} A_{k} A_{k + 1} = J_{k}

(nem egyenlő szárú) háromszöget is az előírt tulajdonságú háromszögekre daraboltuk (itt

A_{k} A_{k + 1}

nem vágandó, mert

J_{k}

határának tekintjük). A felhasznált feltételeket áttekintve látjuk, hogy a következő általánosabb tételt bizonyítottuk be: Minden olyan

A B C

háromszög, melyben a

B

csúcsnál hegyes szög van és ez

k

-szor akkora, mint az

A

csúcsnál levő szög, ‐ ahol

k

az 1-nél nagyobb egész szám, ‐ szétvágható

k - 1

egyenes vágással

k

számú olyan egyenlő szárú háromszögre, hogy valamennyi rész-háromszög szárai egyenlők; a vágásszakaszok hossza a

B C

oldallal egyenlő. (Az első vágást célszerű

C

-ből indítani; de indulhat páros

k

esetén az

A B

oldal, páratlan

k

esetén az

A C

oldal azon

A_{1}

pontjából is, melyre

A A_{1} = B C

.
II. eset: a szárak

B A

és

B C

, a

C

-nél levő szög

φ

. Az állítást

n

párossága szerint két alesetben bizonyítjuk.

II/1. aleset:

n

páratlan. Legyen

n = 2 j - 1

, ahol

j > 1

, egész szám, így a szögek összegéből

φ = 180^{\circ} / (2 j + 1)

. A bizonyítást visszavezethetjük az I. esetre. Mérjük fel az

A B

szárat

A

-tól az

A C

alapra (3. ábra).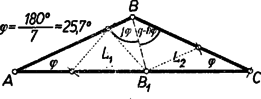

3. ábra

Az előálló

B_{1}

végpont az

A C

szakaszon van, mert

n φ > φ

folytán

A C > A B

. A háromszöget

B B_{1}

mentén kettévágva az

A B B_{1} = L_{1}

és

C B B_{1} = L_{2}

háromszögekre már alkalmazhatjuk a fenti általános tételt. Ugyanis

L_{1}

egyenlő szárú, és a

B B_{1}

alapon levő szögeinek nagysága

(180^{\circ} - φ) / 2 = (2 j + 1 - 1) φ / 2 = j φ = j \cdot p B A B_{1} ∢

. Ennélfogva

L_{2}

-ben

C B B_{1} ∢ = C B A ∢ - B_{1} B A ∢ = (2 j - 1) φ - j φ = (j - 1) φ = (j - 1) \cdot B C B_{1} ∢

. Továbbá a

B

-nél levő részszögek hegyesszögek, mert az

A B B_{1}

szög egy egyenlő szárú háromszögnek alapon levő szöge, a

C B B_{1} ∢ = (j - 1) φ

pedig kisebb

A B B_{1} ∢ = j φ

-nél. A vágásszakasz hossza

L_{1}

és

L_{2}

-ben egyaránt

B B_{1}

, mint az

A

, ill.

C

-nél levő

φ

szöggel szemben fekvő oldal. A vágások száma

1 + (j - 1) + (j - 2) = 2 j - 2 = n - 1

, a létrejövő háromszögek száma pedig

j + (j - 1) = 2 j - 1 = n

, amint bizonyítanunk kellett.
II/2. aleset:

n

páros:

n = 2 j

, ahol

j \geq 1

, egész szám. Vágjuk ketté az

A B C

háromszöget a

B

csúcsból induló

B B_{2}

magasságvonallal (4. ábra).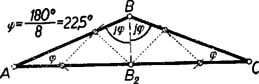

4. ábra

A létrejött egybevágó

A B B_{2}

és

C B B_{2}

derékszögű háromszögek

B

-nél levő szögei hegyesszögek és

n / 2 = j

-szer akkorák, mint az

A

, ill.

C

-nél fekvő szögek. Így a két rész-háromszög a fenti tétel szerint az előírásnak megfelelően feldarabolható (ill.

j = 1

, azaz

n = 2

esetén már fel is van darabolva), tehát az eredeti háromszög is. A vágásszakaszok hossza

B B_{2}

, a vágások száma az egész háromszögben

1 + 2 (j - 1) = 2 j - 1 = n - 1

, és az egyenlő szárú rész-háromszögek száma

2 j = n

az állításnak megfelelően. Ezzel a bizonyítást befejeztük.

Megjegyzés. A feldarabolhatóság bizonyításában az I. esetben a

B

-nél levő

n φ

, szög csúcsából kiinduló vágással is kezdhettük volna vágási sorozatunkat. Így be kellett volna bizonyítanunk, hogy az utolsó vágás utáni maradék-háromszög ugyancsak egyenlő szárú.