Kezdőlap


Feladat:	1959. évi Matematika OKTV II. forduló 3. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1960/január, 5 - 7. oldal		PDF \| MathML
Témakör(ök):	Húrnégyszögek, Thalesz-kör, Háromszögek hasonlósága, OKTV
Hivatkozás(ok):	Feladatok: 1959/szeptember: 1959. évi Matematika OKTV II. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A $Q_{1} Q_{2} Q_{3} Q_{4} Q_{5} Q_{6} = H_{2}$ hatszög bármelyik két egymás utáni oldalát ‐ három egymás utáni csúcsát ‐ az $A B C A' B' C' = H_{1}$ hatszög három egymás utáni oldala ‐ négy egymás utáni csúcsa ‐ határozza meg; és az első és a negyedik csúcs egy átmérőnek két végpontja.

Ezért az állítás első részében elég azt bizonyítanunk, hogy ha

L

M

N

L'

ebben a sorrendben egy

k

körnek egymástól különböző pontjai,

L L'

k

-ban átmérő, és egy a

k

-n fekvő

P

-ből az

L M

M N

N L'

egyenesekre bocsátott merőlegesek talppontjai rendre

Q

R

S

, akkor

Q R = q

és

R S = s

egymásra merőlegesek. Evégett megmutatjuk egyrészt, hogy

P

egy bizonyos

P_{0}

helyzetében

Q_{0} R_{0} = q_{0}

és

R_{0} S_{0} = s_{0}

merőlegesek, másrészt hogy ha

P

elmozdul a

k

-n, akkor

Q R = q

és

R S = s

egymással megegyező irányban ugyanakkora szöggel fordulnak el. (

L

M

N

és

L'

sorrendje megfelel

H_{1}

konvexségének.)
Valóban,

P_{0}

-ként az

M

-en átmenő átmérőnek

M'

másik végpontját véve

Q_{0}

L

-be,

R_{0}

N

-be esik, így

Q_{0} R_{0} S_{0} ∢ = L N S_{0} ∢ = L N L' ∢

, és ez a feltevésnél fogva derékszög.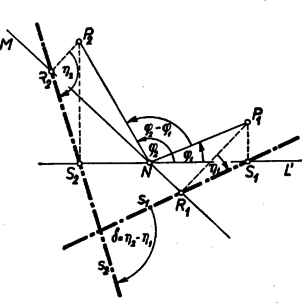

Legyen

η

s

(előjellel vett) hajlásszöge

P R

-nek attól a élegyenesétől mérve, amely

M N

-nek ugyanazon partján van, mint

L

. Az

N

P

R

S

pontok

P

bármely helyzetében húrnégyszöget határoznak meg, ebből látható, hogy

η

mindig egyenlő a

φ = L' N P

szöggel, de avval ellentétes irányú:

η = - φ

. Eszerint ha

P

P_{1}

helyzetből

P_{2}

-be megy át, akkor a megfelelő

s_{1}

-nek

s_{2}

-be való

δ

elfordulási szögét

P_{1} R_{1}

és

P_{2} R_{2}

párhuzamossága folytán az

η_{2} - η_{1}

különbség adja, és erre

δ = η_{2} - η_{1} = - (φ_{2} - φ_{1})

, vagyis

s

elfordulása egyenlő, de ellentétes irányú

N P

elfordulásával. (Ez nem a

k

-n fekvő

P

-re is érvényes.) ‐ Eredményünk alapján egy

P_{2}

-ből szerkesztett

q_{2}

-nek egy

P_{1}

-ből szerkesztett

q_{1}

-hez képest való

ε

elfordulási szöge is kiadódik:

- (ψ_{2} - ψ_{1})

, ahol

ψ_{1}

és

ψ_{2}

ψ = N M P

szög megfelelő két értékét jelöli. ‐ Most már

P

két helyzetének

k

-n

P_{0}

-t és

P

-t véve

ψ - ψ_{0} = P_{0} M P ∢ = P_{0} N P ∢ = φ - φ_{0}

, eszerint

ε = δ

, vagyis

q

s

q_{0}

s_{0}

-hoz képest valóban ugyanannyival és ugyanazon irányban fordulnak el, és ezért

S R Q ∢ = S_{0} R_{0} Q_{0} ∢

, derékszög, amit bizonyítani akartunk.

H_{1}

mindegyik szemben fekvő oldalpárja egymással párhuzamos, mert végpontjaik, mint két átmérő végpontjai, egy téglalapnak a csúcsai; ezért a

P

-ből rájuk bocsátott merőlegesek azonosak, így pl. a

P

Q_{3}

Q_{6}

ponthármas egy egyenesbe esik. Ezért a

Q_{3} Q_{6}

szakasz

F_{3}

felezőpontja egyrészt

P Q_{3}

-on fekszik, másrészt az

A C A' C'

téglalapnak az

A C

-re merőleges tengelyén, amely

k

-nak átmérője, tehát

F_{3}

-ból az

O P

sugár derékszögben látszik,

F_{3}

O P

átmérőjű

k'

Thalész-körnek pontja. (Az utóbbi akkor is áll, ha

F_{3}

éppen

P

-be esik.) Ugyanez áll a

Q_{1} Q_{4}

Q_{2} Q_{5}

szakaszok

F_{1}

F_{2}

felezőpontjára. Ezzel bebizonyítottuk az állítás második részét, és egyben a szóban forgó második kört közvetlen kapcsolatba hoztuk

k

-val és

P

-vel.

II. megoldás: A

H_{1}

hatszög oldalainak merőlegességét a következőképpen is igazolhatjuk. Elegendő

P

-nek a

C' A

íven felvehető helyzeteire szorítkozunk mert

H_{1}

-nek nincs kitüntetett oldala, így a betűzés megváltoztatásával mindig elérhetjük az említett helyzetet. Másrészt elég az egymást

Q_{6}

Q_{1}

Q_{2}

Q_{3}

-ban metsző oldalakra megmutatni, hogy merőlegesek egymásra, mert

H_{1}

csúcsait fordított sorrendben betűzve (

A, B, ..., C'

helyére rendre

C', B', ..., A

-t írva)

Q_{5}

és

Q_{1}

valamint

Q_{4}

és

Q_{2}

felcserélődnek.

Q_{1}

mint a

P A B

háromszög magasság talppontja az

A B

oldal

A

-n túli meghosszabbításán van, mert a

P A B

szög tompaszög, szárai között

k

-nak a

C'

és

C

pontokat tartalmazó, és ezért félkörnél nagyobb

P B

íve fekszik; hasonlóan

Q_{2}

B C

oldal

B

-n túli meghosszabbításának pontja. Ezekből a betűzés megfordításával kapjuk, hogy

Q_{5}

Q_{4}

C' B'

B' A'

oldalnak

C'

-n,

B'

-n túli meghosszabbításán van.

Q_{3}

viszont a

C A'

és

Q_{6}

C' A

szakaszon fekszik, mert a

P C A'

P C' A

háromszögekben

C

-nél és

A'

-nél,

C'

és

A

-nál hegyes szögek vannak. Eszerint

P

H_{2}

-höz viszonyítva a

Q_{6}

Q_{2}

Q_{3}

-nál fekvő (

180^{\circ}

-nál kisebb) szögek terében fekszik, és a

Q_{1}

-nél,

Q_{5}

-nél fekvő egyik-egyik külső szög terében, ezért a

Q_{1}

szög

P Q_{1}

révén két szög különbségeként írható:

Q_{6} Q_{1} Q_{2} ∢ = P Q_{1} Q_{2} ∢ - P Q_{1} Q_{6} ∢

Q_{6}

Q_{2}

Q_{3}

-nál fekvő szögek pedig

P Q_{6}

P Q_{2}

P Q_{3}

-mal két szög összegére bonthatók, pl.

Q_{2} Q_{3} Q_{4} ∢ = Q_{2} Q_{3} P ∢ + P Q_{3} Q_{4} ∢

.
Folytatólag a

P Q_{1} Q_{2} B

és

P Q_{1} A Q_{6}

,,talpponti'' húrnégyszögek, majd a

P A B C

k

-beli'' húrnégyszög révén (mivel bármelyik szög egyenlő a szemben fekvő szög külső szögével)

Q_{6} Q_{1} Q_{2} ∢ = P B C ∢ - P A C' ∢ = P A C ∢ - P A C' = C' A C ∢

, és ez feltevésnél fogva derékszög: a

C C'

átmérő látószöge a

k

-n fekvő

A

pontból. ‐ Majdnem ugyanígy halad a bizonyítás a többi három szög esetében is. A megkezdett példát folytatva:

Q_{2} Q_{3} Q_{4} ∢ = B C P ∢ + P A' B' ∢ = B C P ∢ + P C B' ∢ = B C B' ∢

, ami derékszög. (Olyan, a szereplőkkel egyenlő szögekre térünk át, melyek

H_{1}

csúcsaival vannak meghatározva, majd amelyeknek csúcsuk és egyik száruk közös, és így összegük egyetlen szögként írható.)
Ezzel az állítás első részét bebizonyítottuk.

III. megoldás: Megmutatjuk, hogy

H_{2}

-nek egy oldala a tőle számított második oldallal párhuzamos, és a harmadikra merőleges; ebből már következik, hogy a második és a harmadik oldal egymásra merőleges, vagyis az állítás első része igaz. Valóban, egyrészt pl.

Q_{6} Q_{1}

párhuzamos

Q_{3} Q_{2}

-vel, mert egyenlő szöget alkotnak a

Q_{6} P

(másképpen

Q_{3} P

) félegyenessel:

P Q_{6} Q_{1} ∢ = P A Q_{1} ∢ = P C Q_{2} ∢ = P Q_{3} Q_{2} ∢

továbbá

Q_{1}

és

Q_{2}

P Q_{3}

egyenesnek ugyanazon partján feküsznek. Másrészt

Q_{6} Q_{1}

merőleges

Q_{3} Q_{4}

-re. Ugyanis a

Q_{6}

-nál derékszögű

P A Q_{6}

és a

Q_{3}

-nál derékszögű

A' P Q_{3}

háromszögek hasonlók, mert

P

-nél fekvő hegyes szögeik

P A

és

P A'

merőlegessége folytán egymásnak pótszögei; a

P A Q_{6}

háromszög egy

+ 90^{\circ}

szögű forgatva nyújtással áll elő

A' P Q_{3}

-ból (megfelelők azok a csúcsok, amelyek a két felsorolásnak ugyanannyiadik tagjai). Ugyanez érvényes a

Q_{1}

-nél,

Q_{4}

-nél derékszögű

P A Q_{1}

és

A' P Q_{4}

háromszögekre is, és így a

P Q_{6} A Q_{1}

A' Q_{3} P Q_{4}

, négyszögekre is, mert a hasonlóság aránya mindkét esetben ugyanaz: a

P A

A' P

átfogók aránya. Így

Q_{6} Q_{1}

+ 90^{\circ}

-os forgatva nyújtással áll elő

Q_{3} Q_{4}

-ből (ez többet is mond annál, mint amit állítottunk), ennélfogva

Q_{3} Q_{2}

merőleges

Q_{3} Q_{4}

-re.

Megjegyzés. Egyenesek párhuzamosságára támaszkodik a következő bizonyítás is. Legyen

k

és a

P Q_{6}

egyenes második közös pontja

P^{*}

. Ekkor

C Q_{2} Q_{3} ∢ = C P Q_{3} ∢ = C P P^{*} ∢ = C B P^{*} ∢

, eszerint

P^{*} B

párhuzamos

Q_{3} Q_{2}

-vel. Hasonlóan

P^{*} B' ∥ Q_{3} Q_{4}

, így a

Q_{2} Q_{3} Q_{4}

szög egyállású a

B P^{*} B'

szöggel, ez pedig derékszög.