Kezdőlap


Feladat:	1959. évi Matematika OKTV I. forduló 3. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1959/szeptember, 7 - 8. oldal		PDF \| MathML
Témakör(ök):	Körülírt kör, Magasságvonal, Tengelyes tükrözés, Háromszögek hasonlósága, OKTV
Hivatkozás(ok):	Feladatok: 1959/szeptember: 1959. évi Matematika OKTV I. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyenek az $A B C$ hegyesszögű háromszög magasságvonalainak talppontjai rendre $A_{1}$ , $B_{1}$ , $C_{1}$ . Ezek belső pontjai a $B C$ , $C A$ , ill. $A B$ szakasznak. Ismeretes, hogy hegyesszögű háromszögben az oldalak felezik a talpponti háromszög külső szögeit.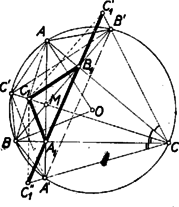

Ennélfogva ha

C_{1}

-nek

C A

, ill.

C B

-re vonatkozó tükörképe

C'_{1}

, ill.

C''_{1}

, akkor a

B_{1} C_{1}

ill.

A_{1} C_{1}

oldalnak

B_{1} C'_{1}

, ill.

A_{1} C''_{1}

tükörképe a

B_{1} A_{1}

oldalnak

B_{1}

, ill.

A_{1}

-en túl való meghosszabbítására esik, tehát

C'_{1} C''_{1}

a talpponti háromszög

k

kerületével egyenlő. Továbbá a tükrözés folytán a

C'_{1} C C''_{1}

háromszög egyenlő szárú:

C C'_{1} = C C_{1} = C C''_{1} = m_{c}

, és

C

-nél levő szöge kétszerese az

A C B

hegyes szögnek. ‐ Az

A B C

háromszög körülírt körének

O

középpontja az

A

B

csúcsokkal együtt a

C' C C''_{1}

-höz hasonló háromszöget alkot, mert

O A = O B = r

, és

A O B ∢ = 2 \cdot A C B ∢

. A hasonlóság folytán:

C' C''_{1} : A B = C C'_{1} : O A

, másképpen

k : c = m_{c} : r

, és ebből

c m_{c} = r k

, ahol a bal oldal az eredeti háromszög

t

területének kétszerese. Így

t = r k / 2

, amit bizonyítanunk kellett.

Megjegyzés. Derékszögű háromszögben a talpponti háromszög elfajul, mert két csúcsa egybeesik a derékszög csúcsával, pl. ha

A C B ∢ = 90^{\circ}

, akkor

A_{1} \equiv B_{1} \equiv C

. Ha a

C C_{1}

szakaszt oda-vissza bejárva elfogadjuk, a ,,háromszög'' ,,kerületének'', akkor a tétel ez esetben is igaz, mert

k = 2 m_{c}

, másrészt

r = c / 2

, ennélfogva

k r / 2 = c m_{c} / 2 = t

.
A bizonyításban felhasznált hasonlóság tompaszögű háromszögben is fennáll ‐ éspedig akár hegyes szög van

C

-nél, akár tompa (természetesen bizonyítása kissé módosul), de a

C'_{1} C''_{1}

szakasz nem a talpponti háromszög

k

kerületét jelenti, hanem a

k - 2 h

különbséget, ahol

h

a talpponti háromszögnek az az oldala, amelynek végpontjai az eredeti háromszög hegyes szögeinek csúcsából húzott magasságok talppontjai. A módosulás magyarázata az, hogy ez esetben csak a leghosszabb oldal egyenese tartja meg a talpponti háromszögben külső szögfelezői szerepét, a másik kettőé belső szögfelezővé válik.

II. megoldás: Ismeretes, hogy a háromszög

M

magasságpontjának az oldalakra, más szóval az

A_{1}

B_{1}

C_{1}

magasságtalppontokra való

A'

B'

C'

tükörképei a körülírt kör kerületén vannak (

A'

C C''_{1}

egyenesen,

B'

C C'_{1}

-n). Így az

A' B' C'

háromszög az

A_{1} B_{1} C_{1}

talpponti háromszögnek az

M

középpontból

2

-szeresre nagyított képe ‐ mert (pl.)

A'

M A_{1}

egyenesen van ‐, és

M A_{1} = A_{1} A'

-ből

M A' = 2 M A_{1}

. Eszerint (pl.)

B' C' = 2 B_{1} C_{1}

. ‐ Hegyesszögű háromszögben az

M

belső pont, ezért tükörképei az

A

-t,

B

-t,

C

-t nem tartalmazó

B C

C A

, ill.

A B

ívre esnek. Az

A C' B A' C B'

(konvex) hatszög területe

2

-szerese az

A B C

háromszög

t

területének, mert annál az

A B C'

B C A'

C A B'

háromszögek együttes területével nagyobb, ez pedig egyenlő

t

-vel, mert tükörképeik:

A B M

B C M

C A M

éppen kitöltik

A B C

-t.
E hatszögnek az

A

B

C

csúcsokba befutó oldalpárjai egyenlők, mert pl.

C A' = C M = C B'

, tehát a körülírt kör

O A'

O B'

O C'

sugaraival való felbontással területét

3

deltoid területének összegeként is előállíthatjuk:

\begin{matrix} 2 t = \frac{O A \cdot B' C'}{2} + \frac{O B \cdot C' A'}{2} + \frac{O C \cdot A' B'}{2} = r B_{1} C_{1} + r C_{1} A_{1} + r A_{1} B_{1} = \\ = r (B_{1} C_{1} + C_{1} A_{1} + A_{1} B_{1}) = r k . \end{matrix}

Evvel igazoltuk a bizonyítandó állítást.

Megjegyzés. Derékszögű háromszögben

M \equiv C \equiv A' \equiv B'

, így a hatszög elfajul, tompaszögű háromszög esetén pedig hurkolttá válik.