Kezdőlap


Feladat:	1958. évi Matematika OKTV II. forduló 3. feladata	Korcsoport: 14-15	Nehézségi fok: könnyű
Füzet:	1958/november, 69 - 71. oldal		PDF \| MathML
Témakör(ök):	Téglalapok, Négyszögek középvonalai, Derékszögű háromszögek geometriája, Pitagorasz-tétel alkalmazásai, OKTV
Hivatkozás(ok):	Feladatok: 1958/október: 1958. évi Matematika OKTV II. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A leírt test négyzetlapja legyen $A B C D$ . A testnek van egy ennek valamelyik oldalával, mondjuk $A B$ -val párhuzamos $E F$ éle, melynek merőleges vetülete a négyzet $A B$ -vel párhuzamos középvonalára esik és azon szimmetrikusan helyezkedik el.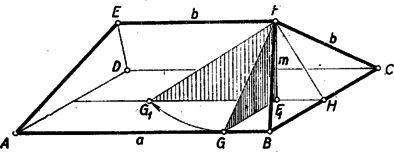

Legyen

F

merőleges vetülete a négyzetlapon, a négyzet

A B

, ill.

B C

oldalán rendre

F_{1}

G

és

H

, jelöljük a négyzet oldalaitól különböző egyenlő élek hosszát

b

-vel, az

F F_{1}

távolságot

m

-mel. Az

F F_{1}

szakasz merőleges

F_{1} G

-re és

F_{1} H

-ra is, így az

F F_{1} G

háromszöget beforgathatjuk körülötte az

E F H

síkba, ekkor

G

egy a

H F_{1}

egyenesen fekvő

G_{1}

pontba kerül. A c) feltétel szerint az

F G_{1} H

háromszög

F

-nél derékszögű,

F F_{1}

pedig a háromszög magassága. Így a magasságra vonatkozó középarányossági tétel szerint, mivel

F_{1} G = a / 2

és

F_{1} H = (a - b) / 2

\begin{matrix} m^{2} = \frac{a}{2} \cdot \frac{a - b}{2} . \end{matrix}

(1)

Számítsuk ki az

A B F E

trapéz

A F

átlóját, mint a páronként merőleges

A G

G F_{1}

F_{1} F

szakaszokból alkotható téglatest testátlóját. Az

E B

átló és a

G D E F

trapéz átlói szimmetria okokból ugyanekkorák. Felhasználva (1)-et is, azt kapjuk, hogy

\begin{matrix} A F^{2} = A G^{2} + G F_{1}^{2} + F_{1} F^{2} = {(\frac{a + b}{2})}^{2} + {(\frac{a}{2})}^{2} + m^{2} = {(\frac{a + b}{2})}^{2} + \\ + {(\frac{a}{2})}^{2} + \frac{a (a - b)}{4} = \frac{1}{4} (3 a^{2} + a b + b^{2}) . \end{matrix}

A feladat állításához azt kell tehát belátnunk, hogy

a b + b^{2} = a^{2}

. Az

a

és

b

élhosszak közt tudunk egy összefüggést kapni, ha felírjuk Pythagoras tételét

F B

-re, mint annak a téglatestnek átlójára, melynek egyik lapja

B G F_{1} H

és egyik további csúcsa

F

. Felhasználva (1)-et is:

\begin{matrix} b^{2} = F B^{2} = B H^{2} + H F_{1}^{2} + F_{1} F^{2} = {(\frac{a}{2})}^{2} + {(\frac{a - b}{2})}^{2} + \frac{a (a - b)}{4} = \end{matrix}

\begin{matrix} = \frac{1}{4} (3 a^{2} - 3 a b + b^{2}) . \end{matrix}

b

-t tartalmazó tagokat a bal oldalra rendezve és

3

-mal osztva innen valóban

\begin{matrix} a b + b^{2} = a^{2} \end{matrix}

adódik és ezzel igazoltuk a feladat állítását.

Megjegyzések: 1. Az utolsó egyenletből

b

-re két érték adódik:

a (\sqrt[]{5} - 1) / 2

és

- a (\sqrt[]{5} + 1) / 2

. Mint egy versenyző, Kalmár Ágota, megjegyezte, a negatív gyöknek is lehet geometriai jelentést tulajdonítani. Ennek egy önmagát átmetsző test felel meg: a két háromszöglap áthatol egymáson, a másik két oldallap pedig hurkolt trapéz lesz

a (\sqrt[]{5} + 1) / 2

oldalhosszúsággal.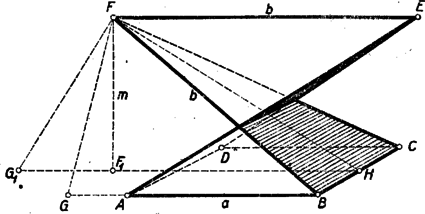

Ugyanekkora az alaplappal párhuzamos él is, míg a trapézok átlói (amelyek most a hurkolt trapézon kívül húzódnak)

a

hosszúságúak.
2. Helyezzük a feladatban szereplő testet egy kocka fölső vízszintes

A B C D

lapjára (

E F

legyen

A B

-vel párhuzamos), majd az

A B R S

-re is helyezzük el a test egy példányát úgy, hogy az

E F

-nek megfelelő él

A S

-sel legyen párhuzamos. Ekkor az

A B

-hez csatlakozó háromszög és trapéz lap a lapszögekre tett kikötés szerint egy síkba esik és egy egyenlő oldalú ötszöget alkot, amely az

E F

felezőmerőlegesére szimmetrikus. A többi kockalapokra is elhelyezhetjük a test egy-egy példányát úgy, hogy egy

12

egybevágó, egyenlő oldalú ötszög határolta poliédert kapjunk. Belátható (erre még visszatérünk), hogy a kapott test egy szabályos dodekaéder.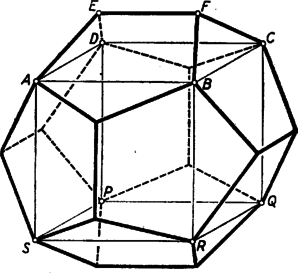