Feladat: 1958. évi Matematika OKTV I. forduló 3. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1958/szeptember, 5 - 6. oldal  PDF  |  MathML 
Témakör(ök): Súlyvonal, Középvonal, Magasságvonal, Paralelogrammák, Pont körüli forgatás, Egyéb sokszögek egybevágósága, OKTV
Hivatkozás(ok):Feladatok: 1958/szeptember: 1958. évi Matematika OKTV I. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyenek a B-ből induló és AB-re, illetve BC-re merőleges négyzet oldalak BD és BE. Forgassuk el a BDE háromszöget B körül 90∘-kal úgy, hogy E a C pontba kerüljön. Ekkor BD az AB oldal meghosszabbításába kerül és azzal egyenlő BD1 szakaszt alkot.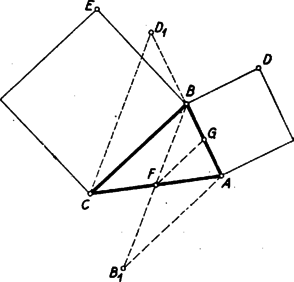

 
 
1. ábra
 

Ennek folytán, ha meghúzzuk az ABC háromszög B-ből induló BF súlyvonalát, az egyben az ACD1 háromszög középvonala is lesz, s így az ED-vel egyenlő CD1 szakasz a BF súlyvonal kétszerese, a feladat állításának megfelelően. Hasonlóan járhatunk el a hatszög másik két szóbajövő oldalával is.
 

Megjegyzések: 1. Azt is tudjuk, hogy BF párhuzamos a CD1 oldallal, s így ED, amiből CD1 egy 90∘-os elforgatással keletkezett, merőleges is a BF súlyvonalra.
Nem egy versenyző észrevette ezt a merőlegességet, de sajnos, fennállását a szemléletből, bizonyítás nélkül elfogadta, holott ez a tény semmivel sem magátólértetődőbb, mint aminek bizonyítását a feladat kívánja.
2. Számos megoldás a fentinek nem lényegesen különböző változata. Így egyesek a B pont F-re vonatkozó B1 tükörképét véve a BDE és ABB1 háromszögek egybevágóságát igazolták, vagy meghúzva a BC-vel párhuzamos FG középvonalat, a BFG és DEB háromszögek hasonlóságát bizonyították fentiekkel rokon gondolatok alapján.
 

II. megoldás: A D és E pontok jelentése legyen ugyanaz, mint az előző megoldásban, és a BDE háromszög B-ből induló magasságvonala messe 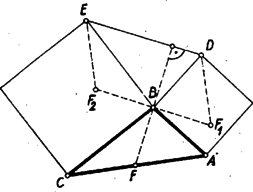AC-t F-ben.
 
 
2. ábra
 

Forgassuk el az ABF és CBF háromszögeket B körül ellenkező irányban 90∘-kal úgy, hogy az A pont D-be, C pedig E-be kerüljön. A háromszögek új helyzete legyen DBF1 és EBF2.
Ekkor az elforgatás következtében a BF1 és BF2 szakaszok merőlegesek BF-re, s így egy egyenesbe esnek, amely párhuzamos ED-vel; másrészt DF1 és EF2 merőleges AC-re, tehát párhuzamos egymással.
Ezek szerint DEF2F1 paralelogramma. Ebből következik egyrészt, hogy DE egyenlő hosszú F1F2-vel, ami BF kétszerese; másrészt az AF-fel egyenlő hosszú DF1 és a CF-fel egyenlő EF2 egymással egyenlők, így tehát BF az ABC háromszög súlyvonala. Ezzel a feladat állítását igazoltuk.
 

III. megoldás: Jelölje D és E ugyanazokat a pontokat, mint az előző megoldásokban. Egészítsük ki az ABC és BDE háromszögeket az ABCB1, ill. BDB2E paralelogrammává.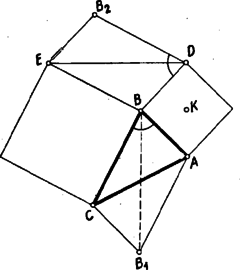
 
 
3. ábra
 

Azt állítjuk, hogy ez a két paralelogramma egybevágó. Forgassuk ugyanis el az ábrát az AB fölötti négyzet K középpontja körül 90∘-kal úgy, hogy AB a BD oldalba menjen át. Ekkor az AB1 oldal, amelyik párhuzamos és egyenlő BC-vel, az utóbbira merőleges BE négyzetoldalra kerül, tehát az ABCB1 paralelogramma BDB2E-t fogja fedni.
Az AC és DE oldalak ennek a paralelogrammának a két átlójával egyenlők s így a paralelogrammában felezik egymást. Ez azonban éppen azt jelenti, hogy a két háromszög bármelyikében a B-vel szemközti oldal a másik B-ből induló súlyvonalának a kétszerese és arra merőleges. Ezzel a feladat állítását (annál valamivel többet is) igazoltuk.
 

Megjegyzések: 1. Ebben a megoldásban világos az ABC és DBE háromszögek teljesen szimmetrikus szerepe, ami különben közvetlenül látszik abból, hogy az ábrán szereplő két négyzet keletkezhetett akár mint az egyik, akár mint a másik háromszög B-ből induló oldalaira kifelé rajzolt négyzet.
2. Ennek megfelelően az I. és II. megoldásban is felcserélhetnénk a két háromszög szerepét, ami annak felel meg, hogy ábráink alapján DE helyett AC-re is igazolhatnánk a feladatnak megfelelő állítást. Ez az I. megoldás esetén teljesen azonos módon történhetne, a II. megoldást annyiban kellene módosítani, hogy BF súlyvonal voltának bizonyítása helyett arra kellene hivatkoznunk, hogy a BDE háromszög B-ből kiinduló súlyvonala egyben a paralelogramma középvonala is, és így DF1-gyel és EF2-vel párhuzamos és egyenlő, a kettő együtt pedig kiadja AC-t.
3. A feladat állítása érvényben marad akkor is, ha nem kifelé, hanem ,,befelé'' rajzolunk az ABC háromszög oldalai fölé négyzeteket. (A hatszög ebben az esetben hurkolt hatszög lesz.) Ez esetben a bizonyításainkban szereplő BDE háromszög helyébe mindössze annak a B pontra vonatkozó tükörképe lép.