Kezdőlap


Feladat:	1957. évi Matematika OKTV II. forduló 3. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1957/szeptember, 7 - 11. oldal		PDF \| MathML
Témakör(ök):	Gúlák, Tetraéderek, Szögfüggvények, síkgeometriai számítások, Egyenlő szárú háromszögek geometriája, Háromszögek hasonlósága, Párhuzamos szelők tétele, Trapézok, Négyszögek középvonalai, OKTV
Hivatkozás(ok):	Feladatok: 1957/szeptember: 1957. évi Matematika OKTV II. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Sok versenyző használt trigonometriát a feladat megoldásában. Bemutatunk egy ilyen megoldást.

I. megoldás. Kiszámítjuk az

S A B C D

gúla térfogatát egyrészt mint az

S A B C

és

S A C D

, másrészt mint az

S A B D

és

S B C D

tetraéderek térfogatának összegét (1. ábra).

1. ábra

S A_{0} B_{0} C_{0} D_{0}

gúla

S

-ből húzott testmagassága egyenlő

α

szögeket zár be a gúla oldaléleivel, és benne van két‐két szemközti oldalél síkjában. Mivel az alaplap négyzet, a kérdéses testmagasság egyben merőleges vetülete is két szemközti oldalél síkjában a másik két oldalélnek. Így egy‐egy ilyen síkkal a másik két oldalél

α

nagyságú szöget zár be.
Jelöljük az

S A

S B

S C

S D

élhosszúságokat

a

b

c

d

-vel.
Az

S A B C

tetraéder alaplapjának az

S A C

háromszöget választva, ennek

S

-nél levő szöge

2 α

, így az

S A

-ra

C

-ből bocsátott magasság hossza

S C

sin 2 α = c sin 2 α

, az alaplap területe tehát

\frac{1}{2} a c sin 2 α

. A

B

csúcsból az alapra bocsátott magasság hossza viszont

b sin α

. Így a tetraéder térfogatát

V_{4}

-gyel jelölve

\begin{matrix} V_{4} = \frac{1}{6} a b c sin 2 α sin α . \end{matrix}

Az első bekezdésben szereplő másik három tetraéder

V_{2}

V_{3}

V_{1}

térfogatára

V_{2} = \frac{1}{6} a c d sin 2 α sin α

V_{3} = \frac{1}{6} a b d sin 2 α sin α

V_{1} = \frac{1}{6} b c d sin 2 α sin α

. A

V_{1} + V_{3} = V_{3} + V_{4}

egyenletet

\frac{1}{6} a b c d sin 2 α sin α

értékkel osztva, a bizonyítandó

\begin{matrix} \frac{1}{a} + \frac{1}{b} = \frac{1}{c} + \frac{1}{d} \end{matrix}

egyenletet kapjuk.

Megjegyzés: Ha a gúla alapja nem négyzet, hanem téglalap, akkor a fenti meggondolásban, csak annyi változik, hogy egy oldalél a két vele szomszédos oldalél síkjával, valamilyen

α

-tól különböző

β

szöget zár be, de ez az érték mind a négy oldalélre ugyanaz. Így a fentiekben a térfogatokban szereplő utolsó tényező

sin α

helyett

sin β

lesz, ami a végkövetkeztetésen nem változtat. A feladat állítása tehát téglalap alapú egyenlő oldalélű gúlára is érvényes.

II. megoldás. A négyszögmetszet

A C

átlója benne van az

S A C

síkban,

B D

átlója pedig az

S B D

síkban, ezen átlók

M

metszéspontja tehát a két sík metszésvonalán van, az pedig az

S A_{0} B_{0} C_{0} D_{0}

gúla

S

-ből induló testmagasságának egyenese, amely az oldalélekkel egyenlő

α

szögeket zár be (1. ábra). Így

S M

közös szögfelezője az

A S C

és

B S D

háromszögeknek, amelyeknek

S

-nél levő szöge egyaránt

2 α

.
Ha e két háromszöget

S M

körül egymásra forgatva képzeljük (ez az egymásra forgatás akkor is elvégezhető, ha az

A_{0} B_{0} C_{0} D_{0}

alaplap téglalap), a feladat állítása a következő síkbeli állítássá fogalmazható át: Ha egy szög felező egyenesének egy pontján át húzott két szelő a szög száraiból a csúcstól számítva a és c, illetőleg b és d hosszúságú szakaszokat metsz le, akkor

\begin{matrix} \frac{1}{a} + \frac{1}{c} = \frac{1}{b} + \frac{1}{d} . \end{matrix}

Ez még úgy is fogalmazható, hogy a szárakból lemetszett szakaszok reciprok értékeinek összege független a szelő irányától. Erre az állításra számos egyszerű, trigonometriát nem használó, megoldás adható.¹⁾
Legyen

A S B

a kérdéses szög, a szögfelező messe az

A B

szakaszt

M

-ben (2. ábra).

2. ábra

Húzzunk

M

-en át párhuzamost

B S

-sel. Messe ez az

S A

-t

N

pontban. Az

S N M

háromszög

S

-nél és

M

-nél fekvő szöge egyaránt

α

, így a háromszög egyenlőszárú. Az egyenlő

S N

és

M N

távolságokat jelöljük

k

-val. Ekkor

A N = a - k

, és a hasonló

A S B

és

A N M

háromszögekből

\begin{matrix} \frac{a}{b} = \frac{a - k}{k} = \frac{a}{k} - 1. \end{matrix}

Mindkét oldalhoz 1-et adva és

a

-val osztva

\begin{matrix} \frac{1}{a} + \frac{1}{b} = \frac{1}{k} . \end{matrix}

Mivel

k

hossza csak az

S M

hosszától és

α

nagyságától függ, az

A B

szelő irányától nem, így állításunkat bebizonyítottuk.

Megjegyzések: 1. Ha tetszés szerinti egyenlő oldalélű gúlát veszünk, akkor az alapsokszög körbeírható, a testmagasság talppontja e kör középpontja, és az oldalélek egyenlő

α

szöget zárnak be a testmagassággal. Ha még az alapsokszög szimmetrikus is a kör középpontjára, vagyis a szemközti csúcsokat összekötő átlók egy ponton, a kör középpontján mennek keresztül, akkor egy síkkal elmetszve ez összes oldaléleket, a keletkező sokszögmetszet szemközti csúcsait összekötő átlók is egy ponton mennek keresztül, és ez a pont a testmagasságon van. Így kiválasztva egy szemközti élpárt a rajtuk átfektetett síkban egy háromszög keletkezik, melyben a

2 α

szög felezőjének hossza a testmagasságnak a metsző síkig terjedő darabja, vagyis mindegyik háromszögben ugyanakkora. Így a bebizonyított tételt alkalmazhatjuk az összes szemközti élpárra és azt kapjuk:
Ha egy egyenlő oldalélű gúla alapja centrálisan szimmetrikus sokszög (és így szükségképpen páros oldalszámú), akkor egy minden oldalélt metsző síkot véve, a szemközti élpárokból lemetszett darabok reciprok értékeinek összege minden élpárra ugyanakkora.
2. A II. megoldásban bizonyított síkbeli tétel következik az 1905. évi Eötvös‐verseny 3. feladatának²⁾ állításából is, mely szerint egy

A B C

háromszög csúcsain át párhuzamosan elmetszve a szemközti oldaelegyeneseket, egy‐egy

A'

B'

C'

pontban, de úgy, hogy

C'

A

és

B

közt legyen (3. ábra) fennáll az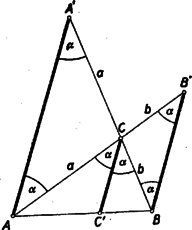

\begin{matrix} \frac{1}{A A'} + \frac{1}{B B'} = \frac{1}{C C'} \end{matrix}

összefüggés.

3. ábra

Ha itt

C C'

C

csúcsú

2 α

szög szögfelezője, akkor az

A C A'

és

B C B'

háromszögek

C

-vel szemközti oldalán fekvő szögei

α

-val egyenlők. Így a két háromszög egyenlő szárú és egymáshoz hasonló. Ezért

A C = C A' = a

B C = C B' = b

és

\begin{matrix} \frac{a}{A A'} = \frac{b}{B B'} = r . \end{matrix}

Innen

A A'

-t és

B B'

-t a fenti egyenletbe helyettesítve

\begin{matrix} \frac{r}{a} + \frac{r}{b} = \frac{1}{C C'}, azaz \frac{1}{a} + \frac{1}{b} = \frac{1}{r \cdot C C'} . \end{matrix}

A jobb oldalon

r

csupán az

α

szög nagyságától függ, így mindazon háromszögekben, amelyek a

2 α

szögben és az ebből induló

C C'

szögfelező hosszában megegyeznek, a

2 α

szöget bezáró oldalak reciprok értékeinek összege egyenlő.

III. megoldás: A feladat állítását a testmagasság segítségül vétele nélkül is bebizonyíthatjuk.
Ha a metsző sík párhuzamos az alappal, akkor az oldalélekből egyenlő szakaszokat metsz le, s így a feladat állítása magától értetődő. Ha ez nem áll, akkor messe egymást, pl.

A B

és

C D

egy

U

pontban (4. ábra).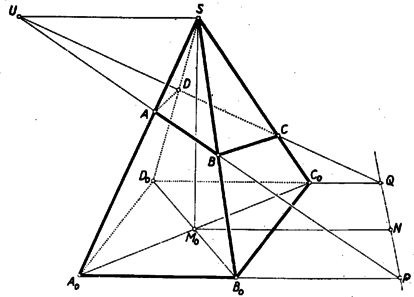

4. ábra

U S

A_{0} B_{0} S

és

C_{0} D_{0} S

síkok metszésvonalán van, ez pedig párhuzamos a két síkban húzható, egymással párhuzamos egyenesekkel, így az

A_{0} B_{0}

és a

C_{0} D_{0}

egyenesekkel. Messe az

A B

A_{0} B_{0}

-t P-ben,

C D

pedig

C_{0} D_{0}

-t

Q

-ban. Az eredeti gúla oldaléleinek közös hosszát jelöljük

e

-vel. Ekkor az

U P

-vel elmetszett

U S

A_{0} P

, és

S A_{0}

egyenesekből álló alakzatból adódik, hogy (5. ábra)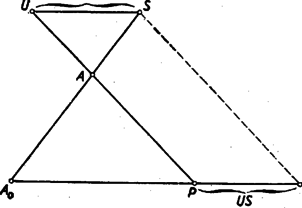

\begin{matrix} \frac{e}{S A} = \frac{A_{0} P + U S}{U S} . \end{matrix}

5. ábra

(Ez közvetlenül világossá válik, ha

S

-ből párhuzamost húzunk

U P

-vel.) Hasonlóan nyerjük, hogy

\begin{matrix} \frac{e}{S B} = \frac{B_{0} P + U S}{U S}, \\ \frac{e}{S C} = \frac{C_{0} Q + U S}{U S}, \frac{e}{S D} = \frac{D_{0} Q + U S}{U S} \end{matrix}

Innen

\begin{matrix} e (\frac{1}{S A} + \frac{1}{S C}) = \frac{A_{0} P + C_{0} Q + 2 U S}{U S}, \\ e (\frac{1}{S B} + \frac{1}{S D}) = \frac{B_{0} P + D_{0} Q + 2 U S}{U S} . \end{matrix}

A_{0} P

és

C_{0} Q

A_{0} P Q C_{0}

trapéz párhuzamos oldalai,

B_{0} P

és

D_{0} Q

pedig a

B_{0} P Q D_{0}

trapéz párhuzamos oldalai, így összegük a megfelelő trapéz középvonalának kétszerese.

A_{0} C_{0}

és

B_{0} D_{0}

azonban egy parallelogramma átlói, s így

M_{0}

metszéspontjuk mindkettőt felezi. Messe az

M_{0}

-ből

A_{0} B_{0}

-vel húzott párhuzamos

P Q

-t az

N

pontban, akkor tehát

M_{0} N

a két trapéz közös középvonala, és így

\begin{matrix} e (\frac{1}{S A} + \frac{1}{S C}) = \frac{2 (M_{0} N + U S)}{U S} = e (\frac{1}{S B} + \frac{1}{S D}), \end{matrix}

amiből a bizonyítandó állítás (

e

-vel osztva) már következik.

Megjegyzések: 1. A bizonyításban hallgatólag feltettük, hogy a

P Q

egyenes nem metszi a gúla alapsokszögét, tehát az

A

B

C

D

pontok egyike sem esik a megfelelő él meghosszabbítására. Ez azonban nem lényeges megszorítás, mert az alapsíkot önmagával párhuzamosan eltolhatjuk addig, míg az összes metszéspontok az alapnégyszögön kívül esnek. Ezzel a metszősík által az élekből lemetszett szakaszok nem változnak, és így a fenti fennálló összefüggések sem. (Egyébként a bizonyítás változtatás nélkül érvényes erre az esetre is, ha az

U S

-sel párhuzamos szakaszokat pozitívnak vagy negatívnak tekintjük, amint irányuk a csúcsok felírt sorrendje szerint megegyezik vagy ellentétes

U S

irányával.)

2. A bizonyításban csak egy helyen használtunk fel az alapról annál többet, hogy parallelogramma: mikor arra következtettünk, hogy a gúla oldalélei egyenlő hosszúságúak. Ha tetszés szerinti parallelogrammát megengedünk alapnak és a gúla csúcsa az átlók metszéspontjában az alapra emelt merőlegesen van, akkor is igaz annyi, hogy

S A_{0} = S C_{0}

(jelöljük hosszukat

e

-vel) és

S B_{0} = S D_{0} (= f)

. Ebben az esetben tehát a fenti levezetés annyit ad, hogy

\begin{matrix} e (\frac{1}{S A} + \frac{1}{S C}) = f (\frac{1}{S B} + \frac{1}{S D}), \end{matrix}

vagyis egy paralelogramma alapú gúlát, amelynek csúcsa az átlók metszéspontjában emelt merőlegesen van, egy síkkal elmetszve, a szemközti élekből lemetszett szakaszok reciprok értékének összege fordított arányban áll egymással, mint a megfelelő élpárok hossza:

\begin{matrix} (\frac{1}{S A} + \frac{1}{S C}) : (\frac{1}{S B} + \frac{1}{S D}) = f : e \end{matrix}

3. Legyenek az

A

B

C

D

pontok merőleges vetületei az alaplapon

A'

B'

C'

D'

. Ezek rendre az

M_{0} A_{0}

M_{0} B_{0}

M_{0} C_{0}

M_{0} D_{0}

félegyenesre esnek, ahol

M_{0}

az alapnégyszög átlóinak metszéspontja (6. ábra).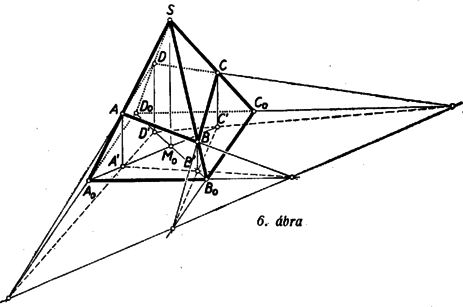

A_{0} B_{0}

A B

A' B'

egy ponton mennek keresztül. Megkeresve a

B_{0} C_{0}

C_{0} D_{0}

és

D_{0} A_{0}

-n a megfelelő metszéspontokat, ezek egy egyenesen, a metszősík és az alapsík metszésvonalán sorakoznak. Könnyen látható, hogy az

M_{0}

pontból a vesszős pontokig terjedő szakaszok közt is fennáll egy olyan összefüggés, amilyen a feladatban szerepel. (Erre vonatkozólag az olvasó a jövő számunkban talál egy kitűzött feladatot.)

¹⁾A feladat az előbbi szövegezésben szerepelt 407. feladatként. Két megoldás található a IV. kötet 4‐5. (1952. májusi) számában a 134‐135. oldalon.
A második formában a feladat lényegében benne foglaltatik a 706. feladatban, amelynek megoldását lásd a XII. kötet 4. (1956. április) számában a 110‐112. oldalon.

²⁾Kürschák J.: Matematikai Versenytételek I. rész. 2. kiadás. 77‐78. old.