Feladat: 1957. évi Matematika OKTV I. forduló 3. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1957/május, 139 - 141. oldal  PDF  |  MathML 
Témakör(ök): Alakzatba írt kör, Deltoidok, Egyenlő szárú háromszögek geometriája, Feuerbach-kör, Középpontos és egyéb hasonlósági transzformációk, Párhuzamos szelők tétele, Párhuzamos szelők tételének megfordítása, OKTV
Hivatkozás(ok):Feladatok: 1957/május: 1957. évi Matematika OKTV I. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Képzeljük a feladatot megoldottnak, a betűzést az 1. ábra mutatja.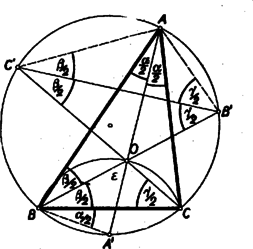

 
 
1. ábra
 

A BO és CO szögfelezők messék a kört másodszor a B', ill. C' pontokban. A kerületi szögek tétele szerint AB'=B'C, és AC'=C'B, és így ugyancsak a kerületi szögek tételének értelmében az OB'AC' négyszögben a B'C' átló felezi a B' és C' csúcspontoknál fekvő szögeket, vagyis a B'C' átló a négyszög szimmetria tengelye. Ebből következik, hogy a négyszög deltoid, és B'C' merőlegesen felezi az AO átlót.
Eszerint az igen egyszerű szerkesztés menete Az AO szakaszt merőlegesen felező egyenes metszi ki a körből a B' és C' pontokat (2. ábra).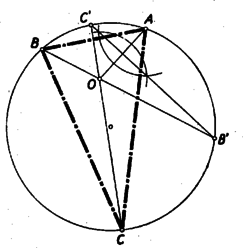
 
 
2. ábra
 

A B'O és C'O egyeneseknek második metszéspontja a körrel szolgáltatja a keresett B, ill. C pontokat.
 

II. megoldás: Még egyszerűbb szerkesztéshez jutunk a következőképpen: Legyen az AO egyenes második metszéspontja a körrel A'. Az A'BO▵-ben a O csúcsnál fekvő ϵ szög az AOB▵ külső szöge (1. ábra). Tehát ϵ=α2+β2. Az A'BC∢ mint kerületi szög α2, és így az A'BO∢=α2+β2=ϵ. Tehát az A'BO▵-ben e két egyenlő szöggel szemben fekvő két oldal is egyenlő, vagyis
A'B=A'O,hasonlóanA'C=A'O.

Eszerint az A' körül A'O sugárral rajzolt kör metszi ki az adott, körből a keresett B és C pontokat (3. ábra).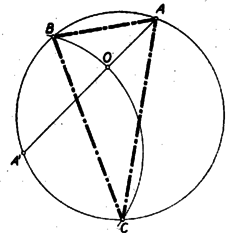
 
 
3. ábra
 

Megjegyzés: Az itt bizonyított tételt (mely szerint a háromszög köré írt kör két csúcspont közti ívének felezőpontja éppolyan távol van a két csúcsponttól, mint a háromszögbe írt kör középpontjától) lényegében tartalmazta az 1954. évi Arany Dániel versenyen kezdők részére kitűzött 1. feladat (lásd a K. M. L. IX. kötet, 2. sz. 1954. okt., 33. o.), de megtalálható a tétel a Matematikai Versenytételek I. részében is az 1897/2. feladathoz fűzött 2. jegyzetében (42. o.). Néhány versenyző hivatkozott is e forrásokra, de a megoldók zöme bizonyította e tételt.
A bizonyítás tulajdonképpen már az I. megoldásban megtörtént, amikor megmutattuk, hogy az OB'AC' négyszög (1. ábra) deltoid, vagyis B'A=B'O, és C'A=C'O.
 

III. megoldás: Igen szép, szellemes megoldáshoz jutunk (bár nem a legegyszerűbbhöz), ha az előzőknél valamivel többet (Feuerbach-féle kör) használunk fel.
Tekintsük a keresett ABC▵-et valamely A'B'C'▵ talpponti háromszögének, akkor az adott K középpontú és r sugarú k kör az A'B'C'▵ Feuerbach-féle köre (K≡F'). Ismeretes, hogy az A'B'C'▵ magasságvonalai a talpponti háromszög szögfelezői, tehát az adott O pont azonos az A'B'C' háromszög M' magasságpontjával, A pedig az A'-ból kiinduló magasságvonal A'1 talppontja. Ismeretes továbbá, hogy az A'B'C'▵ k' körülírt köre nem egyéb, mint a k Feuerbach-féle körnek 1:2 arányú kivetítése az M'(≡O) centrumból.
Eszerint a szerkesztés menete: Az O(≡M') pont tükörképe a K(≡F') pontra nézve lesz az A'B'C'▵ köré írt k' körnek K' középpontja (4. ábra).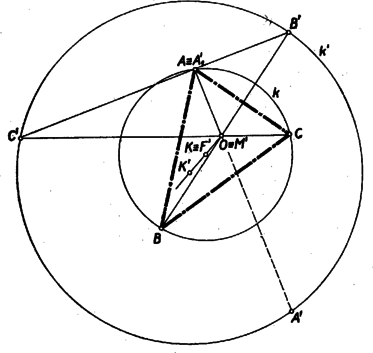
 
 
4. ábra
 

K' körül 2 r sugárral rajzolt kör a k' kör. Az A(≡A'1) pontban OA(≡M'A'1)-ra emelt merőleges egyenes metszi ki a k'-ből a B' és C' pontokat. A B'O(≡B'M') és C'O(≡C'M') egyeneseknek a k körrel való, O(≡M') ponton túl fekvő metszéspontjai a keresett B és C pontok.
 

IV. megoldás: Könnyen nyerhető egy szerkesztés, de távolról sem egyszerű szerkesztés, Euler egy tételén keresztül, melyet a versenyzők nagy része ismert és felhasznált, pl. a következő módon:
Ha az adott kör középpontja K, sugara r, a keresett ABC háromszögbe írt kör sugara ϱ, és OK=d, akkor Euler tétele szerint (lásd pl. Matematikai Versenytételek I. rész, 41. o.)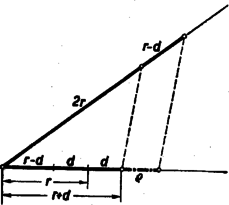
2rϱ=r2-d2=(r+d)(r-d)
ahonnan
2r:(r+d)=(r-d):ϱ,
és így ϱ az adatokból negyedik arányosként könnyen megszerkeszthető (5. ábra).
 
 
5. ábra
 

Az A pontból az O körül ϱ sugárral rajzolt körhöz szerkesztett érintők metszik ki az adott körből a keresett B és C pontokat (6. ábra).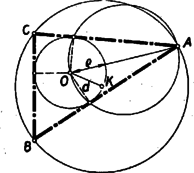
 
 
6. ábra
 

Az idézett helyen megtaláljuk annak bizonyítását is, hogy az Euler-összefüggés teljesülése esetén a kerület bármely A pontjából indulva ki a BC egyenes is érinti az O középpontú ϱ sugarú kört, tehát az ABC háromszög megfelel a feladat feltételeinek.
Mindig van egy és csakis egy megoldás, mert 2r>r+d miatt r-d>ϱ, és így a ϱ sugarú kör mindig az r sugarú kör belsejében van.1
 

Megjegyzés: E tétel különben, mint láthattuk (gyakorlati szempontból tekintve) elég körülményes szerkesztéshez vezet, még akkor is, ha negyedik arányosként szerkesztjük meg közvetlenül a ϱ-t. A megoldók legnagyobb része azonban ügyetlenebbül a d2=r(r-2ϱ) alakból, az adott d és r szakaszokból, a derékszögű háromszöggel kapcsolatos mértani középarányosság felhasználásával szerkesztette meg az r-2ϱ szakaszt, amelyből r-(r-2ϱ)2-ként kapta meg a ϱ-t.
1Szerkesztő megjegyzése: Számos versenyző ‐ főleg lapunk olvasói ‐ használta fel e tételt, amelyre lapunk a közelmúltban kétszer is (XIII. kötet 3. sz. 1956. november, 96. o., és XIII, kötet 5. sz. 1956. december 143. o.) hivatkozott. Kitűnik ebből, hogy a középiskolai matematikai irodalom ismerete kétségkívül előnyt jelent a versenyzőknek, amint erre lapunk állandóan rámutatott.
Jelen esetben azonban sem az Euler-tételre, sem a Feuerbach-féle körre nem volt szükség, hanem az I. gimnáziumban tanult egyszerű szögösszefüggések vezettek el a legegyszerűbb, legelegánsabb szerkesztéshez, amint azt az I. és II. megoldásban láttuk.