Kezdőlap


Feladat:	1956. évi Matematika OKTV II. forduló 1. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1956/szeptember, 5 - 7. oldal		PDF \| MathML
Témakör(ök):	Hozzáírt körök, Érintősokszögek, Háromszögek hasonlósága, Beírt kör, OKTV
Hivatkozás(ok):	Feladatok: 1956/szeptember: 1956. évi Matematika OKTV II. forduló 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Az $a_{1}$ , $b_{1}$ , $c_{1}$ szakaszok által az adott $A B C ▵$ -ből lemetszett háromszögek nyilvánvalóan hasonlóak az $A B C ▵$ -höz. A jelölést az 1. ábra mutatja.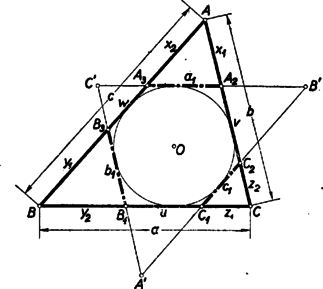

1. ábra

Ennek alapján

\begin{matrix} x_{1} : b = a_{1} : a \end{matrix}

amiből

\begin{matrix} x_{1} = \frac{a_{1}}{a} b . \end{matrix}

Hasonlóképpen

\begin{matrix} x_{2} = \frac{a_{1}}{a} c, y_{1} = \frac{b_{1}}{b} c, y_{2} = \frac{b_{1}}{b} a, z_{1} = \frac{c_{1}}{c} a, z_{2} = \frac{c_{1}}{c} b . \end{matrix}

A B C ▵

kerülete:

\begin{matrix} (u + v + w) + (x_{1} + x_{2}) + (y_{1} + y_{2}) + (z_{1} + z_{2}) = k . \end{matrix}

Az érintő hatszög tétele szerint

\begin{matrix} u + v + w = a_{1} + b_{1} + c_{1}, \end{matrix}

és így

\begin{matrix} (a_{1} + b_{1} + c_{1}) + \frac{a_{1}}{a} (b + c) + \frac{b_{1}}{b} (a + c) + \frac{c_{1}}{c} (a + b) = \\ = a_{1} + b_{1} + c_{1} + \frac{a_{1}}{a} (k - a) + \frac{b_{1}}{b} (k - b) + \frac{c_{1}}{c} (k - c) = \\ = a_{1} + b_{1} + c_{1} + \frac{a_{1}}{a} k + \frac{b_{1}}{b} k + \frac{c_{1}}{c} k - a_{1} - b_{1} - c_{1} = \\ = k (\frac{a_{1}}{a} + \frac{b_{1}}{b} + \frac{c_{1}}{c}) = k . \end{matrix}

Mindkét oldalt

k

-val osztva a bizonyítandó összefüggést kapjuk.

II. megoldás: Az előző megoldásban szereplő

\begin{matrix} y_{2} = \frac{b_{1}}{b} a, z_{1} = \frac{c_{1}}{c} a \end{matrix}

összefüggéseket fogjuk felhasználni, emellett megmutatjuk, hogy

\begin{matrix} a_{1} = u . \end{matrix}

Ebből már következik az állítás, ha az

\begin{matrix} a = y_{2} + u + z_{1} = \frac{b_{1}}{b} a + a_{1} + \frac{c_{1}}{c} a \end{matrix}

összefüggést

a

-val osztjuk.
A bizonyítandó egyenlőség igazolására hosszabbítsuk meg az

a_{1}

b_{1}

c_{1}

egyeneseket, míg metszik egymást. A keletkező

A' B' C' ▵

oldalai párhuzamosak az

A B C ▵

megfelelő oldalaival, és beírt körük közös. Így a kiegészített ábra centrálszimmetrikus a beírt kör

O

középpontjára nézve. Tehát az

u

és

a_{1}

szakaszok is egymás tükörképei

O

-ra nézve, amivel állításunkat igazoltuk.

III. megoldás: Egészítsük ki az ábrát az

A B

oldalt és a másik két oldal meghosszabbítását érintő körrel (2. ábra).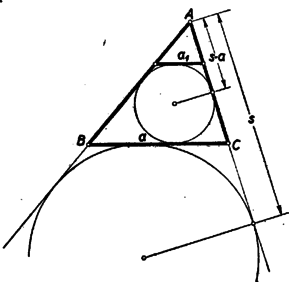

2. ábra

A háromszög kerületét

2 s

-sel jelölve tudjuk, hogy a

C

csúcsból a két körhöz húzott érintő szakaszok hossza

s - a

és

s

. A beírt kör a

C

csúcsnál az

a_{1}

szakasszal levágott kis háromszögnek hozzáírt köre. Így e kis háromszögből és körből álló ábrarész hasonló az

A B C

háromszögből és hozzáírt köréből álló ábrarészhez. A kettőben egymásnak megfelelő szakaszok aránya tehát egyenlő. Így

\begin{matrix} \frac{a_{1}}{a} = \frac{s - a}{s} . \end{matrix}

Hasonlóan

\begin{matrix} \frac{b_{1}}{b} = \frac{s - b}{s}, \frac{c_{1}}{c} = \frac{s - c}{s} . \end{matrix}

Ezeket összeadva

\begin{matrix} \frac{a_{1}}{a} + \frac{b_{1}}{b} + \frac{c_{1}}{c} = \frac{3 s - (a + b + c)}{s} = \frac{3 s - 2 s}{s} = 1. \end{matrix}

Megjegyzések: 1. Néhány versenyző rámutatott, hogy tételünk a hozzáírt kör esetén is érvényes, ha a keletkező szakaszokat előjellel vesszük. Egy még messzebb menő általánosítást adott Udvari András. Megfogalmazásához először is tekintsünk két párhuzamos szakaszt egyező vagy ellenkezű előjelűnek aszerint, amint a két szakasz kezdőpontjától a végpont felé mutató irány megegyezik, vagy ellentétes.
Legyen egy

A B C

háromszögnek valamely, a síkjában fekvő,

P

pontjára vonatkozó tükörképe

A' B' C' ▵

és jelölje

A' B'

metszéspontját

B C

-vel és

C A

-val

C_{1}

, illetőleg

C_{2}

-vel,

B' C'

metszéspontját

C A

-val és

A B

-vel

A_{2}

ill.

A_{3}

, végül

C' A'

metszéspontját

B A

ill.

B C

-vel

B_{3}

, ill.

B_{1}

-gyel, ekkor

\begin{matrix} \frac{A_{2} A_{3}}{C B} + \frac{B_{3} B_{1}}{A C} + \frac{C_{1} C_{2}}{B A} = 1. \end{matrix}

(1)

Az 1. ábrában a

P

szerepét

O

tölti be; ez esetben mind a három arányszám pozitív és az (1) helyességét az I., II., III. megoldásokban bebizonyítottuk.
Az általános esetet a 3. ábra mutatja.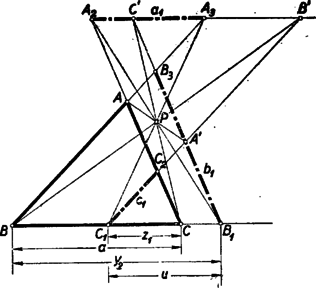

3. ábra

Mivel a pontra való tükrözés egy szakaszt ugyanakkora, de ellenkező előjelű szakaszba visz át:

\begin{matrix} \frac{A_{2} A_{3}}{C B} = - \frac{A_{2} A_{3}}{B C} = \frac{B_{1} C_{1}}{B C}, \\ \frac{B_{3} B_{1}}{A C} = \frac{B B_{1}}{B C}, \\ \frac{C_{1} C_{2}}{B A} = \frac{C_{1} C}{B C} . \end{matrix}

E három egyenlőség összeadásából adódik

\begin{matrix} \frac{A_{2} A_{3}}{C B} + \frac{B_{3} B_{1}}{A C} + \frac{C_{1} C_{2}}{B A} = \frac{B_{1} C_{1} + B B_{1} + C_{1} C}{B C} = \frac{B B_{1} + B_{1} C_{1} + C_{1} C}{B C} = \frac{B C}{B C} = 1. \end{matrix}

2. Egy térbeli általánosításra mutatott rá Zsombok Zoltán. Lásd a 772. sz. feladatot a 29. oldalon.