Feladat: 1956. évi Matematika OKTV I. forduló 2. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1956/május, 131 - 133. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Trapézok, OKTV
Hivatkozás(ok):Feladatok: 1956/május: 1956. évi Matematika OKTV I. forduló 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen AB az adott szakasz és e az adott egyenes. Vetítsük az AB szakaszt egy tetszőleges O pontból az e egyenesre, a DC szakaszba. Az ABCD pontok egy trapéz csúcspontjai. Ismeretes, hogy a trapéz nem-párhuzamos oldalainak metszéspontját az átlók metszéspontjával összekötő egyenes felezi a trapéz párhuzamos oldalait.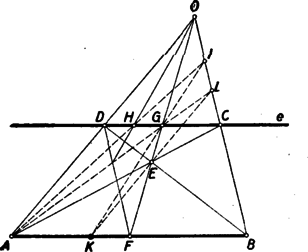

 
 
1. ábra
 

Az 1. ábrán az O pontot a trapéz AC és BD átlóinak E metszéspontjával összekötő egyenes az AB, illetve CD szakaszt az F, illetve G felezési pontokban metszi. Az ABCD trapézzal kapcsolatosan most végzett szerkesztésnek az AFGD trapézre való megismétlésével nyerjük a DG szakasz felezési pontját, a H pontot. Tehát a HG szakasz a HC szakasznak harmadrésze. Messe az AH egyenes az OB egyenest az I pontban, az I és G pontok összekötő egyenese az AB szakaszt a K pontban. Mivel az I pontból a HG és GC szakaszokat AK és KB szakaszokba vetítjük, ezért az AK szakasz az AB szakasznak harmadrésze. (Itt 10 egyenes vonalat használtunk fel a K pont szerkesztéséhez.)
 

Megjegyzés: Ha az O pont és e egyenes az AB szakasz által el vannak választva; akkor előfordulhat, hogy AH∥OB (vagyis az I pont a végtelenbe kerül), akkor a G pontnak az AH (ill. OB) egyenessel párhuzamos vetülete szolgáltatja az AB szakaszon a keresett K pontot.
 

II. megoldás: Ha már megszerkesztettük a CD szakasz G felezési pontját, akkor egyszerűbben is célt érünk. Messe az A és G pontokat összekötő egyenes az OB egyenest az L pontban, akkor megmutatjuk, hogy az LE egyenes és az AB szakasz K metszéspontjára AK az AB szakasz harmadrésze (1. és 2. ábra).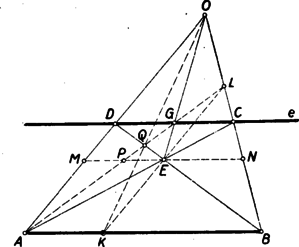
 
 
2. ábra
 

Ugyanis képzeljünk a trapéz átlóinak E metszéspontján át a párhuzamos oldalakkal párhuzamos egyenest, amely az OA és OB egyeneseket az M, illetve N pontban metszi (2. ábra). Ha az AG egyenes az utóbbi párhuzamost P pontban metszi, akkor MP=PE, mivel ezek a szakaszok az egymással egyenlő DG és GC szakaszoknak vetületei A-ból a párhuzamosra. Azonban ismeretes, hogy ME=EN, tehát PE a PN szakasz harmadrésze. Mivel végül L-ből a PE és EN szakaszokat az AK és KB szakaszokba vetítjük, ezért az AK szakasz valóban az AB szakasz harmadrésze. (Itt már 7 egyenessel célhoz jutottunk.)
 

Megjegyzés: Itt ugyanúgy előfordulhat mint az I. megoldásban, hogy AG∥ ∥OB. Ez esetben az E-nek AG-vel (ill. OB-vel) párhuzamos vetülete az AB szakaszon a keresett K pont.
 

III. megoldás: Ugyancsak 7 egyenest igényel a következő szerkesztés. A CD szakasz G felezőpontjának megszerkesztése után az AG és BD szakaszok Q metszéspontját kötjük össze az O ponttal (2. és 3. ábra). Az OQ egyenes metszi ki az AB szakaszból a keresett K harmadoló pontot.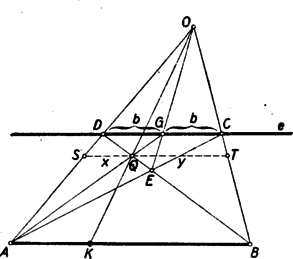
 
 
3. ábra
 

Bizonyítás: Legyen CG=GD=b. Messe a Q ponton átmenő AB-vel párhuzamos egyenes az OA és OB egyeneseket az S, ill. T pontban (3. ábra). Legyen SQ=x, QT=y. A szögek egyenlősége miatt AQSΔ∼AGDΔ, BQTΔ∼BDCΔ, ABQΔ∼GDQΔ.
Ennek alapján
x:b=AQ:AG=BQ:BD=y:2b,
amiből
y=2x,
és így az y és x szakaszokat O-ból az AB szakaszra vetítve a keletkező szakaszokra
KB=2AK.