Kezdőlap


Feladat:	1955. évi Matematika OKTV II. forduló 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1955/szeptember, 8 - 13. oldal		PDF \| MathML
Témakör(ök):	Mértani helyek, Súlyvonal, Magasságvonal, Háromszögek hasonlósága, Egyenesek egyenlete, OKTV
Hivatkozás(ok):	Feladatok: 1955/szeptember: 1955. évi Matematika OKTV II. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

3. feladat a) része

I. megoldás: Vizsgáljuk meg az

A B C_{▵}

B C = a

oldalán nyugvó beírt téglalapok középpontjainak mértani helyét. Legyen egy ilyen téglalap

P_{1} P_{2} P_{3} P_{4}

. A betűzést az 1. ábra mutatja.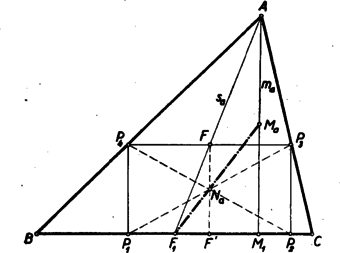

1. ábra

P_{3} P_{4}

oldal

F

felezőpontja, mint ismeretes, rajta van az

A F_{1} = s_{a}

súlyvonalon.

F F'

a téglalap

P_{1} P_{2}

oldalára merőleges (tehát az

A M_{1}

magasságvonallal párhuzamos) középvonala. A téglalap

N_{a}

középpontja e középvonal felezőpontja, és így rajta van az

A M_{1} F_{1}

derékszögű háromszög

F_{1} M_{a}

súlyvonalán, ahol

M_{a}

A M_{1} = M_{a}

magasság felezőpontja.

Megfordítva legyen

N_{a}

F_{1} M_{a}

szakasz tetszés szerinti belső pontja.Tegyük fel, hogy a háromszög nem egyenlőszárú. Húzzunk az

N_{a}

ponton át az

a

egyenesre merőleges egyenest, legyen ennek az

a

és az

A F_{1}

egyenesek közé eső szakasza

F' F

. Ennek

N_{a}

felezőpontja, mert az

A F_{1} M_{1}

háromszög

F_{1} M_{a}

súlyvonalán van és

F' F

párhuzamos az

A B

C háromszög

A M_{1}

magasságával. Hasonlóan látható, hogy az

F

pont felezi a rajta át

a

-val párhuzamosan húzott egyenesnek az

A C

és

A B

vonalak közé eső

P_{3} P_{4}

szakaszát. A végpontokból az a egyenesre

P_{3} P_{2}

és

P_{4} P_{1}

merőlegeseket bocsátva tehát olyat téglalapot kapunk, amelynek

N_{a}

a középpontja és amely az

A B C

háromszögbe van írva a kívánt módon. Több ilyen téglalap nem lehetséges, mert ha a

P_{3} P_{4}

oldalt közelítjük az

a

oldalhoz, illetőleg távolítjuk attól, akkor a középpont is közeledik, illetőleg távolodik, tehát különbözni fog

N a

-tól.

Ha az

A B C

háromszög egyenlőszárú (

A B = A C

), akkor a szimmetria alapján könnyen látható (2. ábra), hogy a téglalapok középpontjai az

M_{1} M_{a}

szakaszra esnek, másrészt ennek bármely

N_{a}

belsőpontjára tükrözve az

M_{1} (= F_{1})

pontot, az

F

tükörképen át

a

-val párhuzamosan húzott egyenesnek a szárakkal való metszéspontjaiból az

a

oldalra bocsátott merőlegesek ismét egy kívánt tulajdonságú téglalapot adnak.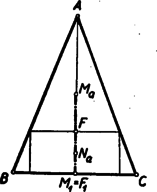

2. ábra

F_{1}

és

M_{a}

végpontokhoz tartozó téglalapok az

a

oldallá, illetőleg az

M_{a}

magasságvonallá fajulnak.
A keresett mértani hely tehát az

F_{1} M_{a}

szakasz.

II. megoldás: A téglalap középpontja felfogható a másik,

P_{1} P_{2}

-vel párhuzamos,

F_{b} F_{c}

középvonal felezőpontjaként is (3. ábra).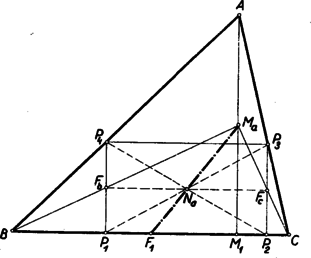

3. ábra

Nyilvánvaló, hogy

F_{b}

, mint

P_{1} P_{4}

felezőpontja rajta van az

A M_{1} B

derékszögű háromszőg

B M_{a}

súlyvonalán,

F_{c}

pedig az

A M_{1} C

háromszög

C M_{a}

súlyvonalán. Így az

F_{b} F_{c}

középvonal

N_{a}

felezöpontja rajta van a

B M_{a} C_{▵}

-nek

M_{a} F_{1}

súlyvonalán.
Ismét könnyen látható a gondolatmenet megfordításával, hogy az

F_{1} M_{a}

szakasz minden pontjához tartozik pontosan egy kívánt elhelyezkedésű téglalap, amelynek a kiszemelt pont a középpontja.

\begin{matrix} * \end{matrix}

Mint a fenti két megoldásból látható, a keresett mértani hely teljesen elemi úton, minden koordináta‐geometria nélkül meghatározható. Minthogy igen sok versenyző használt koordináta‐geometriát, mégpedig legtöbbnyire igen ügyetlenül, és gyakran még a helyes eredménynek sem tudott geometriai értelmet adni, azért itt közlünk egy egyszerű megoldást koordináta‐geometriában.

III. megoldás: Helyezzük el hegyesszögű háromszögünket a derékszögű koordinátarendszerben úgy, hogy a

B C

oldal az

x

tengelyre, az

A

csúcspont a pozitív tengelyre kerüljön. A betűzést a 4. ábra mutatja.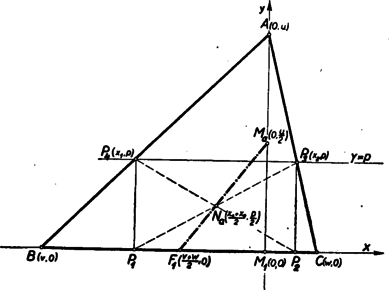

4. ábra

Legyen a

P_{3} P_{4}

téglalapoldal egyenlete

y = p

, a

P_{4}

pont koordinátái (

x_{1}, p

) és

P_{3}

ponté (

x_{2}, p

) akkor

N_{a}

, a téglalap középpontjának koordinátái

x_{a} = \frac{x_{1} + x_{2}}{2}

y_{a} = \frac{p}{2}

A B

egyenes egyenlete

\begin{matrix} y = - \frac{u}{v} x + u, azaz u x + v y = u v, \end{matrix}

(1)

A C

egyenes egyenlete

\begin{matrix} y = - \frac{u}{w} x + u, azaz u x + w y = u w, \end{matrix}

(2)

y

helyébe a

P_{3}

illetőleg

P_{4}

pont

p

ordinátáját írva, (1)-ből, illetőleg (2)-ből

x

értékül

x_{1}

-et, illetőleg

x_{2}

-t kell kapnunk, tehát

\begin{matrix} u x_{1} + v p = u v és u x_{2} + w p = u w . \end{matrix}

A kettőt összeadva

\begin{matrix} u (x_{1} + x_{2}) + (v + w) p = u (v + w) \end{matrix}

Mivel

x_{1} + x_{2}

és

p

N_{a}

pont

x_{a}

és

y_{a}

koordinátáinak kétszeresei, így azt kaptuk, hogy e koordinátákra

\begin{matrix} 2 u x_{a} + 2 (v + w) y_{a} = u (v + w), \end{matrix}

(3)

vagyis (explicit alakra térve át)

N_{a}

koordinátái kielégítik az

\begin{matrix} y = - \frac{u}{v + w} (x - \frac{v + w}{2}) \end{matrix}

egyenletet, feltéve, hogy

v + w \neq 0

.
Ez az egyenes átmegy a

(\frac{v + w}{2}, 0)

ponton, vagyis a

B C

oldal

F_{1}

felezőpontján, és iránytangense

- \frac{u}{v + w} = - \frac{u}{2} : \frac{v + w}{2}

, de ez nem más, mint

F_{1}

-ből a

(0, \frac{u}{2})

pontba, a magasságvonal

M_{a}

felezőpontjába vivő egyenes iránytangense. Az

N_{a}

pont tehát ezen az egyenesen mozog, és mivel

p

pozitív és

u

-nál kisebb, így

y_{a}

pozitiv és

\frac{u}{2}

-nél kisebb,

x_{a}

pedig

\frac{v + w}{2}

és 0 között változik, mert

y_{a}

két szélső érlékéhez

x_{a} = \frac{v + w}{2}

(ha

y_{a} = 0

), illetőleg

x_{a} = 0

(mikor

y_{a} = \frac{u}{2}

) értékek tartoznak.
A keresett mértani hely tehát az

F_{1} M_{a}

szakasz.
Ha

v + w = 0

, vagyis egyenlőszárú a háromszög, akkor (3)-ból

\begin{matrix} x_{a} = 0, \end{matrix}

továbbá most is

0 < y_{a} < \frac{u}{2}

. A mértani hely tehát most is az

F_{1} M_{a} (= M_{1} M_{a})

szakasz.

Megjegyzés: Ha megengedjük, hogy a beírt téglalapok csúcspontjai a háromszögoldalak meghosszabbításán is lehetnek, akkor a háromszög tompaszögű is lehet, és a mértani hely a teljes

F_{1} M_{a}

egyenes.

3. feladat b) része

I. megoldás: A téglalap köré írt kör középpontja a téglalap középpontja, a téglalap átlója pedig átmérője a körnek. Így a keresett téglalapok középpontjának közösnek kell lennie, átlóiknak pedig egyenlőknek ‐ ha vannak egyáltalán ilyen téglalapok.
Két téglalap közös középpontja a feladat a) része szerint csak két háromszögoldalhoz meghatározott mértani helyek közös pontja lehet. Mivel az adott háromszög feltétel szerint hegyesszögű, a magasságvonalak

M_{a}

M_{b}

, és

M_{c}

felezőpontjai az oldalközéppontok alkotta

F_{1} F_{2} F_{3}

háromszög oldalainak belső pontjai (5. ábra), az

F_{1} M_{a}

és

F_{2} M_{b}

szakaszok tehát e háromszög transzverzálisai, s így metszik egymást egy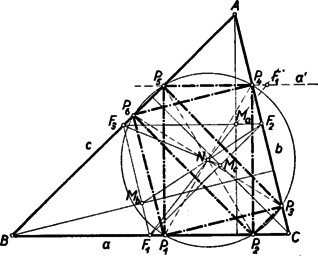

N

pontban.

5. ábra

Legyen az

A B C

háromszögbe írt

N

középpontú és

a

oldalon nyugvó téglalap

P_{1} P_{2} P_{4} P_{5}

. Tudjuk, hogy van ilyen téglalap és csak egy.
A

P_{1}

és

P_{4}

pontok, mint átlóvégpontok, egymás tükörképei az

N

pontra vonatkozóan. Mivel pedig a

b

egyenesnek csak egy olyan pontja van, amelynek

N

-re vonatkozó tükörképe a

B C

egyenesen van, így

P_{4}

ez a pont.
Az

N

pont rajta van az

F_{2} M_{b}

egyenesen is, tehát írható az

A B C

háromszögbe olyan

N

középpontú téglalap is, amelyik a

b

oldalon nyugszik. Ennek egyik

b

-n levő csúcsával átellenes csúcs az

a

oldalon lesz és ezek egymás tükörképei az

N

pontra nézve, így az előző megjegyzés szerint e csúcspárt csak a

P_{4}

és

P_{1}

pontok adhatják. Legyen a kérdéses

b

oldalon nyugvó beírt téglalap

P_{3} P_{4} P_{6} P_{1}

. Ekkor a

P_{3} P_{6} = P_{1} P_{4}

, mint a téglalap átlói, továbbá

P_{1} P_{4} = P_{2} P_{5}

, mint a

P_{1} P_{2} P_{4} P_{5}

téglalap átlói. Mindhárom átlót felezi az

N

pont.
Ekkor a

P_{5} P_{6} P_{2} P_{3}

négyszög átlói is felezik egymást és egyenlők, tehát a négyszög téglalap; az

A B C

háromszögbe írt olyan téglalap, amelynek

N

a középpontja és egyik oldala az

A B = c

háromszögoldalon van. A három téglalap középpontja közös, átlóik egyenlők, tehát körülírt körük közös.
A feladat a) része I. megoldásának második felét is figyelembe véve, a fenti gondolatmenet módot ad a téglalapok megszerkesztésére is (5. ábra). Ilyen téglalap‐hármas csak egy lehet, mert az

N

pont egyértelműen meg van határozva, ennek helyzete pedig egyértelműen meghatározza a téglalapokat.
Mivel

N

középpontja mindhárom téglalapnak, eredményünkből az is következik, hogy az

F_{1} M_{a}

F_{2} M_{b}

F_{3} M_{c}

mértani helyek egy ponton mennek keresztül.

II. megoldás: A mértani helyek felhasználása nélkül is megoldható feladatunk. Ha a

P_{1} P_{3} P_{5 ▵}

-et tekintjük (5. ábra), akkor látjuk, hogy a

P_{1}

-nél levő szög, mint merőleges szárú szög, egyenlő az

A B C_{▵}

-nek

C

-nél fekvő

γ

szögével. Ugyanezen oknál fogva a

P_{1} P_{3} P_{5} ∢ = α

, és

P_{3} P_{5} P_{1} ∢ = β

, és így

\begin{matrix} P_{3} P_{5} P_{1 ▵} \sim A B C_{▵} . \end{matrix}

P_{6} P_{2} P_{4}

háromszög a

P_{3} P_{5} P_{1}

háromszögnek a köréjük írt kör középpontjára vonatkozó tükörképe. Ezt a megfigyelést felhasználva a következőképpen szerkeszthetünk a keresett ábrához hasonlót (amit azután alkalmasan elforgatva és kicsinyítve már könnyen megszerkeszthetjük a keresett téglalapokat).
Rajzoljunk az

A B C_{▵}

köré kört; ebben a csúcsokkal átellenes pontok legyenek

A'

B'

C'

(6. ábra).

6. ábra

A C'

B A'

C B'

egyenesek alkotta

A_{0} B_{0} C_{0 ▵}

oldalai merőlegesek az

A B C_{▵}

megfelelő oldalaira, s így a két háromszög hasonló.

A B A' B'

B C B' C'

és

C A C' A'

az előbbi háromszögbe beírt téglalapok, mert átlóik (mint körátmérők) felezik egymást és egyenlők. Így valóban a keresett ábrához hasonlót nyertünk. (Magát a szerkesztést természetesen mindjárt az

A_{0} B_{0} C_{0} ▵

megrajzolásával kezdhetjük; a szerkesztés igazolását szolgáló segédvonalak a szerkesztéskor elhagyhatók).

III. megoldás: A

P_{1}

P_{6}

P_{5}

és

P_{4}

pontok ismeretében (5. ábra) a másik kettő könnyen szerkeszthető (pl. mint

P_{6}

és

P_{5}

tükörképe a

P_{1} P_{4}

szakasz felezőpontjára). E négy pont viszont

P_{1}

ismeretében úgy szerkeszthető, hogy belőle

a

-ra merőlegest állítunk, illetőleg

b

-vel párhuzamost húzunk. Az előbbinek

c

-vel való

P_{6}

metszéspontjából párhuzamost húzunk

a

-val, az utóbbinak

c

-vel való

P_{6}

metszőpontjából merőlegest állítunk

b

-re. A kettő

P_{4}

-ben metszi egymást.

Ha egy pontot sem ismerünk, akkor az

a

oldal tetszésszerinti

Q_{1}

pontjából kiindulva végezzük el az éppen leírt szerkesztést, a keletkezett metszéspontok legyenek sorra

Q_{5}

Q_{6}

Q_{4}

(7. ábra).

7. ábra

Egészítsük ki

Q_{6} Q_{5} Q_{4}

-et egy

Q_{2}

csúccsal,

Q_{1} Q_{6} Q_{4}

-et pedig egy

Q_{3}

csúccsal téglalappá.

Q_{2}

nyilván

a

-n van, a

Q_{3}

-an és

Q_{4}

-en átmenő

b'

egyenes pedig párhuzamos

b

-vel. A keletkezett téglalapok

Q_{2} Q_{5}

, illetőleg

Q_{3} Q_{6}

átlói egyenlők a közös

Q_{1} Q_{4}

átlóval és felezik egymást annak felezőpontjában. Ebből viszont következik, hogy

Q_{5} Q_{6} Q_{2} Q_{3}

is téglalap, mert átlói felezik egymást és egyenlő hosszúak. Az

a

b'

és

c

oldalak az adott háromszöghöz hasonló és hasonló helyzetű háromszöget alkotnak

B

-vel mint hasonlósági ponttal. Így a keresett ábrához hasonlót kaptunk.

Q_{4}

-et

B

-ből

b

-re vetítve nyerjük a

P_{4}

pontot és ebből kiindulva már megszerkeszthetjük a továbbiakat. (A szerkesztés elvégzésekor

Q_{4}

után természetesen mindjárt

P_{4}

-et szerkesztjük. A szerkesztés megtalálását és egyben mindjárt helyességének igazolását is szolgáló segédvonalak és pontok megrajzolására a szerkesztéskor nincs szükség.)

Megjegyzések: 1. A feladat a) részéhez fűzött megjegyzésből kitűnik, hogy ha a beírt téglalap csúcspontjaira semmi kikötést nem teszünk, akkor tompaszögű háromszög esetén is megoldható feladatunk b) része.
2. Derékszögű háromszög esetén (pl. ha

γ = 90^{\circ}

)

F_{1} \equiv M_{b}

és

F_{2} \equiv M_{a}

, és így

M_{c} \equiv N

P_{5} \equiv P_{6}

P_{2} \equiv P_{3} \equiv C

. Ez esetben tehát a befogókhoz tartozó téglalapok azonosak, az átfogóhoz tartozó téglalap pedig az

m_{c}

magasságvonallá fajul.
3. Tehát minden háromszögnek van egy és csakis egy

N

pontja.