Kezdőlap


Feladat:	1955. évi Matematika OKTV I. forduló 2. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1955/május, 132 - 134. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Középpontos tükrözés, Paralelogrammák, OKTV
Hivatkozás(ok):	Feladatok: 1955/május: 1955. évi Matematika OKTV I. forduló 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyenek a keletkezett részháromszögeknek az adott háromszög $a$ oldalával párhuzamos oldalai rendre $a_{1}$ , $a_{2}$ , $a_{3}$ és ezen oldalakhoz tartozó magasságok $m_{1}$ , $m_{2}$ , $m_{3}$ . Nyilvánvaló, hogy $a_{1} + a_{2} + a_{3} = a$ , és az is könnyen belátható, hogy $m_{1} + m_{2} + m_{3} = m$ (1. ábra), ahol $m$ az adott háromszögnek $a$ oldalához tartozó magassága.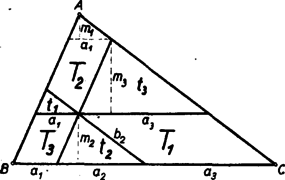

1. ábra

Tehát az adott háromszög területét

T

-vel jelölve

\begin{matrix} 2 T = a m = (a_{1} + a_{2} + a_{3}) (m_{1} + m_{2} + m_{3}) = \\ a_{1} m_{1} + a_{2} m_{2} + a_{3} m_{3} + (a_{1} m_{2} + a_{2} m_{1}) + (a_{1} m_{3} + a_{3} m_{1}) + (a_{2} m_{3} + a_{3} m_{2}) & (1) \end{matrix}

2 t_{1} = a_{1} m_{1}

és

2 t_{2} = a_{2} m_{2}

; e két egyenlőség szorzata

\begin{matrix} 4 t_{1} t_{2} = a_{1} m_{1} a_{2} m_{2} = (a_{1} m_{2}) (a_{2} m_{1}) \end{matrix}

(2)

Mivel a részháromszögek ‐ a szögek egyenlősége miatt ‐ mind hasonlók az adott háromszöghöz, és így egymás között is, azért

\begin{matrix} \frac{a_{1}}{a_{2}} = \frac{m_{1}}{m_{2}}, vagyis a_{1} m_{2} = a_{2} m_{1} . \end{matrix}

Tehát (2) alapján

\begin{matrix} {(a_{1} m_{2})}^{2} = {(a_{2} m_{1})}^{2} = 4 t_{1} t_{2}, \end{matrix}

amiből

\begin{matrix} a_{1} m_{2} = a_{2} m_{1} = 2 \sqrt[]{t_{1} t_{2}}, vagyis a_{1} m_{2} + a_{2} m_{1} = 4 \sqrt[]{t_{1} t_{2}} . \end{matrix}

Ugyanígy mutatható meg, hogy

\begin{matrix} a_{1} m_{3} + a_{3} m_{1} = 4 \sqrt[]{t_{1} t_{3}} és a_{2} m_{3} + a_{3} m_{2} = 4 \sqrt[]{t_{2} t_{3}} . \end{matrix}

Ezen értékeket (l)-be helyettesítve, és 2-vel osztva

\begin{matrix} T = t_{1} + t_{2} + t_{3} + 2 \sqrt[]{t_{1} t_{2}} + 2 \sqrt[]{t_{1} t_{3}} + 2 \sqrt[]{t_{2} t_{3}} = {(\sqrt[]{t_{1}} + \sqrt[]{t_{2}} + \sqrt[]{t_{3}})}^{2} . \end{matrix}

Megjegyzés: Ha a keletkezett 3 paralelogramma területeit

T_{1}

T_{2}

T_{3}

-mal jelöljük, amint azt az ábra mutatja, akkor az ábrából közvetlenül leolvasható, hogy

\begin{matrix} a_{1} m_{2} (= 2 \sqrt[]{t_{1} t_{2}}) = T_{3}, a_{3} m_{2} (= 2 \sqrt[]{t_{2} t_{3}}) = T_{1}, \end{matrix}

és könnyen belátható (kis területi átalakítás után), hogy

\begin{matrix} a_{1} m_{3} = (= 2 \sqrt[]{t_{1} t_{3}}) = T_{2}, \end{matrix}

Eszerint a fenti eredmény a

T = t_{1} + t_{2} + t_{3} + T_{1} + T_{2} + T_{3}

egyenlőség alapján adódik.
Az itt felhasznált összefüggések közvetlen igazolásán (mégpedig a hasonlóság felhasználása nélkül) alapszik a következő megoldás.

II. megoldás: Tekintsük először az ábrának

t_{1}

t_{3}

és

T_{2}

alkotta részét. A betűzést a 2. ábra mutatja.

2. ábra

Egészítsük ki az

A B_{1} C_{1}

háromszöget, a

B_{1} C_{1}

oldal felezőpontjára tükrözve, paralelogrammává és hosszabbítsuk meg a

B_{2} P

és

C_{2} P

szakaszokat a paralelogramma szemközti oldaláig. Ekkor

\begin{matrix} B_{1} C_{1} A_{▵} ≅ C_{1} B_{1} A_{▵}^{'}, P B_{1} C_{2 ▵} ≅ B_{1} P B_{2 ▵}^{'}, C_{1} P B_{2 ▵} ≅ P C_{1} C_{2 ▵}^{'} \end{matrix}

és így a

C_{2} A B_{2} P

paralelogramma

T_{2}

területe megegyezik a

B_{2}^{'} A^{'} C_{2}^{'} P

paralelogrammáéval. Az előbbinek

P B_{2} = c_{3}

, oldalához tartozó magassága egyenlő a

t_{1}

háromszög

c_{1}

oldalához tartozó

m'_{1}

magasságával; az utóbbi paralelogramma

P B_{2}^{'} = c_{1}

oldalához tartozó magassága pedig a

t_{3}

háromszög

c_{3}

oldalához tartozó

m'_{3}

magasságával. Tehát

\begin{matrix} T_{2} = c_{3} m_{1} = c_{1} m'_{3}, \end{matrix}

amiből

\begin{matrix} T_{2}^{2} = c_{1} m_{1}' c_{3} m_{3}' = 4 t_{1} t_{3}, vagyis T_{2} = 2 \sqrt[]{t_{1} t_{3}} . \end{matrix}

Hasonlóképpen adódik, hogy

\begin{matrix} T_{1} = 2 \sqrt[]{t_{2} t_{3}}, T_{3} = 2 \sqrt[]{t_{1} t_{2}}, \end{matrix}

és így

\begin{matrix} T = t_{1} + t_{2} + t_{3} + 2 \sqrt[]{t_{2} t_{3}} + 2 \sqrt[]{t_{3} t_{1}} + 2 \sqrt[]{t_{1} t_{2}} = {(\sqrt[]{t_{1}} + \sqrt[]{t_{2}} + \sqrt[]{t_{3}})}^{2} . \end{matrix}

III. megoldás: Legegyszerűbben úgy jutunk célhoz, ha felhasználjuk azt az ismeretes tételt, mely szerint hasonló háromszögek területei úgy aránylanak egymáshoz, mint a megfelelő oldalak négyzete.
Tehát

\begin{matrix} \sqrt[]{t_{1}} : \sqrt[]{T} = a_{1} : (a_{1} + a_{2} + a_{3}), \\ \sqrt[]{t_{2}} : \sqrt[]{T} = a_{2} : (a_{1} + a_{2} + a_{3}), \\ \sqrt[]{t_{3}} : \sqrt[]{T} = a_{3} : (a_{1} + a_{2} + a_{3}) . \end{matrix}

Összeadva

\begin{matrix} \frac{\sqrt[]{t_{1}}}{\sqrt[]{T}} + \frac{\sqrt[]{t_{2}}}{\sqrt[]{T}} + \frac{\sqrt[]{t_{3}}}{\sqrt[]{T}} = \frac{a_{1} + a_{2} + a_{3}}{a_{1} + a_{2} + a_{3}} = 1, \end{matrix}

ahonnan,

\begin{matrix} \sqrt[]{t_{1}} + \sqrt[]{t_{2}} + \sqrt[]{t_{3}} = \sqrt[]{T}, \end{matrix}

vagyis

\begin{matrix} T = {(\sqrt[]{t_{1}} + \sqrt[]{t_{2}} + \sqrt[]{t_{3}})}^{2} . \end{matrix}