Kezdőlap


Feladat:	1954. évi Matematika OKTV II. forduló 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1954/szeptember, 8 - 12. oldal		PDF \| MathML
Témakör(ök):	Középponti és kerületi szögek, Tengelyes tükrözés, Rombuszok, Középpontos és egyéb hasonlósági transzformációk, Húrnégyszögek, Háromszögek hasonlósága, OKTV
Hivatkozás(ok):	Feladatok: 1954/szeptember: 1954. évi Matematika OKTV II. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A betűzést az 1.ábra mutatja.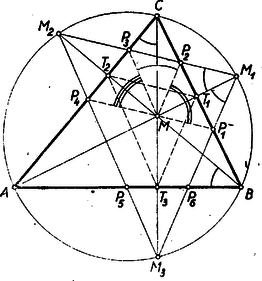

1. ábra

Először egy segédtételt bizonyítunk be. Ismert tétel alapján (Gallai-Péter I. oszt.tankönyv 1953 ‐ 302. old.) az

M_{1}

M_{2}

M_{3}

pontok rajta vannak az

A B C_{Δ}

köré írt körön. Mint merőlegesszárú szögek a

B

-nél levő egyíves szög egyenlő a

C

-nél levő egyíves szöggel, vagyis a kerületi szögek tétele alapján

\hat{M_{2} A} = \hat{A M_{3}}

és így az

M_{1} A

egyenes felezi az

M_{1} M_{2} M_{3 Δ}

M_{1} ∢

-ét. Ugyanez áll az

M_{2} B

és

M_{3} C

egyenesekre is az

M_{2} ∢

, illetőleg

M_{3} ∢

-ge1 kapcsolatban.
Ennek felhasználásával a feladat állítása így bizonyítható: Kössük össze az

M

pontot a keletkezett hatszög

P_{1}

P_{2}

P_{3}

és

P_{4}

csúcspontjaival. Az

M P_{1} M_{1} P_{2}

négyszögben a

P_{1} P_{2}

átló a tükrözés miatt felezi a

P_{1}

és

P_{2}

csúcspontoknál levő szögeket. Tehát a szóban forgó négyszögben a két átló egymásra merőleges és a segédtétel alapján mindkét átló egyúttal szögfelező, amiből következik, hogy az

M P_{1} M_{1} P_{2}

négyszög rombusz, és így

P_{1} M ∥ M_{1} P_{2}

. Hasonlóképpen az

M P_{4} M_{2} P_{3}

rombuszban

P_{4} M ∥ M_{2} P_{3}

.
De az

M_{1} P_{2}

és

M_{2} P_{3}

szakaszok rajta vannak az

M_{1} M_{2}

egyenesen, amellyel a

P_{1} M

és

P_{4} M

szakaszok külön-külön párhuzamosak. A két utóbbi szakasznak egy közős pontja

M

, és így

P_{1}

M

és

P_{4}

egy egyenesen vannak, vagyis a

P_{1} P_{4}

átló átmegy az

M

ponton. Ugyanígy bizonyítható ez a

P_{2} P_{5}

, ill.

P_{3} P_{6}

átlóra is.

Megjegyzés: Igen sok versenyző ‐ a segédtétel nélkül ‐ az átlók merőlegességéből és csak egyedül a

P_{1} P_{2}

átló szögfelező voltából már rombuszra következtetett, megfeledkezvén a deltoidról.

II. megoldás: Segédtételünkhöz a háromszög köré írt kör nélkül is eljuthatunk. Ugyanis, ha az adott

A B C_{Δ}

-nek

T_{1} T_{2} T_{3}

talpponti háromszögét tekintjük (1. ábra), akkor nyilván az

M_{1} M_{2} M_{3 Δ}

a talpponti háromszögnek 2 : 1 arányú nagyítása az

M

hasonlósági centrumból. Elég most már arra az ismert tételre hivatkozni (Gallai-Péter I. oszt. Tankönyv 1953 ‐ 287-288. old.), hogy a háromszög magasságvonalai a talpponti háromszög szögfelezői.
Lényegében ezzel azonos bizonyítás: az

M_{1}, M_{2}

és

M_{3}

pontokon át a

B C

C A

, ill.

A B

oldalakkal húzott párhuzamos egyenesek által alkotott

A_{1} B_{1} C_{1 Δ}

-ben alkalmazzuk a talpponti háromszögre vonatkozó idézett tételt.

III. megoldás: Segédtételünk alapján

P_{2} T_{1} = T_{1} P_{1}

P_{3} T_{2} = T_{2} P_{4}

M_{1} T_{1} = T_{1} M

(1. ábra). Az

M_{1}

P_{2}

és

P_{3}

pontok az

M_{1} M_{2}

egyenesen vannak, a

T_{1} T_{2}

egyenes pedig párhuzamos az

M_{1} M_{2}

egyenessel, azért a

P_{1}

P_{4}

és

M

pontok rajta vannak az

M_{1} M_{2}

egyenesnek a

T_{1} T_{2}

egyenesre vonatkozó tükörképén, vagyis

P_{1}

P_{4}

és

M

egy egyenesen vannak.

IV. megoldás: Jelöljük az

M_{1} M_{2} M_{3 Δ}

szögeit

M_{1} ∢

M_{2} ∢

, ill.

M_{3} ∢

-gel. Mivel ‐ mint láttuk ‐

M P_{1} M_{1} P_{2}

és

M P_{4} M_{2} P_{3}

rombuszok (1. ábra), azért az

M

-nél fekvő két, ill. három ívvel jelölt szögek egyenlők

M_{1} ∢

ill.

M_{2} ∢

-gel. Az

M

-nél fekvő áthúzott ívvel jelölt szög pedig mint megfelelő szög, egyenlő

M_{3} ∢

-gel. Tehát a

P_{1} M P_{4} ∢ = M_{1} ∢ + M_{2} ∢ + M_{3} ∢ = 180^{\circ}

, vagyis

P_{1}

M

és

P_{4}

egy egyenesen van.

V. megoldás: Húzzunk az

M

ponton át párhuzamost az

M_{1} M_{2}

oldallal. Messe ez

M_{1} M_{3}

-at

D

-ben,

M_{2} M_{3}

-at

E

-ben. (2. ábra).

2. ábra

A segédtétel alapján következik, hogy

D M M_{1} ∢ = M M_{1} M_{2} ∢ = M M_{1} M_{3} ∢

, tehát az

M M_{1} D_{Δ}

egyenlőszárú, s így

D

M M_{1}

felező merőlegesén van. E felező mérőleges azonban a

B C

egyenes, tehát

D

M_{3} M_{1}

és

B C

egyenesek metszéspontja, vagyis a hatszög egyik csúcsa

(D = P_{1})

. Hasonlóan következik, hogy

E

C A

és

M_{2} M_{3}

oldalak metszéspontja, amely a hatszögnek

D

-vel átellenes pontja

(E = P_{4})

. Az ezeket összekötő átló tehát valóban

M

-en megy keresztül. Hasonlóan okoskodhatunk a többi átlókkal is. (Lényegében ez a gondolata Pátkai György bizonyításának).
A segédtétel felhasználása nélkül, közvetlenül az

M_{1}

M_{2}

M_{3}

pontokon átmenő kör segítségével is bizonyíthatjuk állításunkat, amint azt a VI ‐ IX. megoldások mutatják.

VI. megoldás: Kössük össze az

M

pontot a hatszög

P_{3}

és

P_{6}

csúcspontjával (3. ábra).

3. ábra

A B M_{1} C

húrnégyszögben

A ∢ + M_{1} ∢ = 180^{\circ}

. Tehát az

A

csúcsnál lévő, az ábrán egy ívvel, ill. két ívvel és az

M_{1}

csúcsnál egyszer áthúzott, ill. kétszer áthúzott ívvel jelölt szögek, (szám szerint 4) összege

180^{\circ}

.
Az

A

-nál levő egyíves szög, mint kerületi szög egyenlő az

M_{3}

-nál lévő egyíves szöggel, ez pedig a tükrözés folytán egyenlő az

M

-nél levő egyíves szöggel. Teljesen ugyanígy bizonyítható, hogy az

A

-nál lévő kétíves szög egyenlő az

M

-nél lévő kétíves szöggel. Az

M_{1}

-nél lévő egyszer áthúzott ívvel jelölt szög, mint tükrös szög, ill. csúcsszög egyenlő az

M

-nél fekvő hasonló jelzésű szöggel. Ugyanez áll az

M_{1}

-nél és

M

-nél lévő kétszer áthúzott ívvel jelölt szögekre is. De a

P_{3} M P_{6} ∢

éppen e négyféle szög összege, vagyis

P_{3} M P_{6} ∢ = 180^{\circ}

. Ezzel bebizonyítottuk, hogy a

P_{3} P_{6}

átló átmegy az

M

ponton. (Tomor Benedek megoldása.)

VII. megoldás: Kössük össze az

M

pontot a hatszög

P_{2}

és

P_{5}

csúcspontjával. Be fogjuk bizonyítani, hogy a

B P_{2} M P_{5}

négyszögben az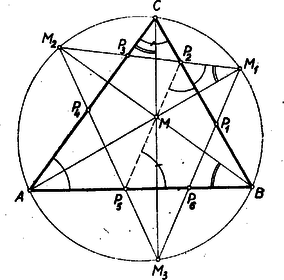

M ∢ = 180^{\circ}

(4. ábra).

4. ábra

P_{2}

-nél lévő egyíves szögek a tükrözés miatt egyenlők. Ennek a szögnek pótló szöge az

M_{1}

-nél fekvő kétíves szög, amely, mint kerületi szög, egyenlő a

B

-nél fekvő kétíves szöggel, ez viszont mint merőlegesszárú szög, egyenlő a

C

-nél fekvő kétíves szöggel. Ez utóbbi pótlószöge az

A

-nál fekvő egyíves szögnek. Tehát négyszögünk

P_{2} ∢

-e egyenlő az

A B C_{Δ} A ∢

-ével. Ugyanígy bizonyíthatjuk, hogy négyszögünk

P_{5} ∢

-e(az ábrán egyszer áthúzott ívvel jelölve) egyenlő az

A B C_{Δ} C ∢

-ével. Tehát négyszögünkben

B ∢ + P_{2} ∢ + P_{5} ∢ = B ∢ + A ∢ + C ∢ = 180^{\circ}

, és így a negyedik szög:

M ∢ = 180^{\circ}

. (Bártfai Pál megoldása.)

VIII. megoldás: Kössük össze az

M

pontot a hatszög

P_{3}

és

P_{6}

csúcspontjával (5. ábra).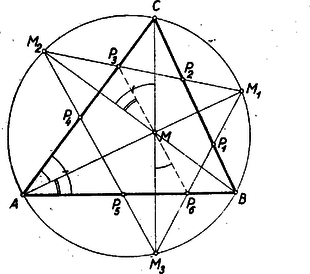

5. ábra

A

-nál fekvő egyíves, ill. kétíves szög a VI. megoldás alapján egyenlő az

M

-nél fekvő hasonló jelzésű szögekkel. E két szög összege az

A

-nál fekvő egyszer áthúzott ívvel jelölt szög, amely mint merőleges szárú szög, egyenlő az

M

-nél fekvő egyszer áthúzott ívvel jelölt szöggel, amiből következik, hogy a

P_{3} M C

egyenlő az egyíves szöggel, vagyis

P_{3} M C ∢

és

P_{6} M M_{3} ∢

csúcsszögek. Tehát a

P_{3} P_{6}

átló átmegy az

M

ponton.

IX. megoldás: Kössük össze az

M

-et a hatszög

P_{1}

és

P_{4}

csúcspontjával, továbbá

C

-t

M_{1}

és

M_{2}

-vel 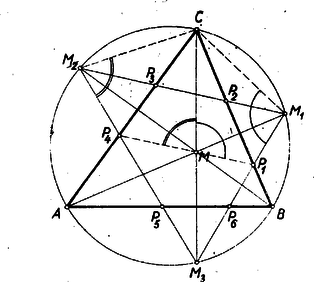(6. ábra).

6. ábra

M_{1}

-nél lévő egyíves szög a tükrözés folytán egyenlő az

M

-nél lévő egyíves szöggel. Ugyanígy egyenlők az

M_{2}

és

M

-nél lévő kétíves szögek. De az

M_{1} C M_{2} M_{3}

húrnégyszögben a

M_{1} ∢ + M_{2} ∢ = 180^{\circ}

, tehát a

P_{1} M P_{4} ∢ = 180^{\circ}

. (Reichlin-M. Viktor megoldása.)
Az állítás következő, igen szellemes, csupán a talpponti háromszög tulajdonságain alapuló bizonyítását adta Vigassy József, a verseny győztese.

X. megoldás: Kössük össze az

M

pontot a hatszög

P_{3} P_{2} P_{1}

és

P_{6}

csúcsaival, továbbá húzzuk meg az

A B C_{Δ}

-ben az

M

-en át az

A B

-vel párhuzamos

A' B'

és az

A C

-vel párhuzamos

A'' C''

szakaszt (7. ábra).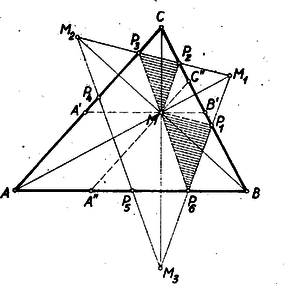

7. ábra

A keletkezett

A' B' C

és

A'' B C''

háromszögek hasonlók és hasonló fekvésűek. A tükrözés folytán az

M P_{3} P_{2}

, ill.

P_{6} M P_{1 Δ}

-ek a fenti két háromszögbe írt minimális kerületű háromszögek (Gallai Péter I. oszt. Tankönyv 1953 ‐ 332-334. old.), vagyis a talpponti háromszögek, melyek tehát egymásközt szintén hasonlók és hasonló fekvésűek. Tehát

M P_{3} ∥ P_{6} M_{1}

, mint megfelelő oldalak. E két párhuzamos szakasznak

M

végpontja közös, ennélfogva a

P_{6}

M

és

P_{3}

pontok egy egyenesbe esnek.

Megjegyzés: Tételünk tompaszögű háromszögre is általánosítható, de akkor a megfelelő

P_{1} P_{2} P_{3} P_{4} P_{5} P_{6}

pontok hurkolt hatszögre vezetnek, melynek kétszeres pontja (hurokpontja) mindenkor a tompaszög csúcspontja. A szemközt fekvő csúcspontok most is a

P_{1}

és

P_{4}

P_{2}

és

P_{5}

P_{3}

és

P_{6}

csúcspontok (8.ábra).

8. ábra

A bizonyítás ugyanúgy történik, minta hegyesszögű háromszög esetén, csakhogy most a tompaszöget bezáró oldalokhoz tartozó magasságok (melyeknek talppontjai az oldalak meghosszabbítására esnek) a talpponti háromszög külső szögét felezik, vagyis a tompaszöget bezáró oldalak felezik a talpponti háromszög megfelelő szögeit. Az

M

hasonlósági centrum e szerepét most is megtartja.