Kezdőlap


Feladat:	1954. évi Matematika OKTV II. forduló 1. feladata	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1954/szeptember, 5 - 6. oldal		PDF \| MathML
Témakör(ök):	Szögfüggvények, síkgeometriai számítások, Koszinusztétel alkalmazása, Trigonometriai azonosságok, OKTV
Hivatkozás(ok):	Feladatok: 1954/szeptember: 1954. évi Matematika OKTV II. forduló 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A megoldás lényege annak észrevétele volt, hogy a feltételi egyenletből következik, hogy a $γ$ szög értéke $120^{\circ}$ . Ehhez lényegében két úton juthatunk: vagy a szögeket küszöböljük ki távolságok segítségével és azután felhasználjunk a háromszög alkotórészei közötti összefüggéseket, vagy az adott összefüggést goniometriai összefüggéssé igyekszünk alakítani és goniometriai átalakításokat végzünk. Az előbbi út pl. a következő módon követhető.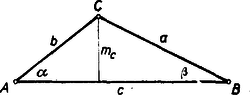

I. megoldás: A betűzést az ábra mutatja. Helyettesítsük be az adott összefüggésbe a

sin α = \frac{m_{c}}{b}, sin β = \frac{m_{c}}{a}, 2 t = c m_{e}

kifejezéseket és emeljünk négyzetre. Mivel mindkét oldalon pozitív mennyiség áll, az eredetivel ekvivalens összefüggéshez jutunk

\begin{matrix} c^{2} m_{c}^{2} = a^{2} b^{2} (\frac{m_{c}^{2}}{a^{2}} + \frac{m_{c}^{2}}{b^{2}} + \frac{m_{c}^{2}}{a b}) = (a^{2} + b^{2} + a b) m_{c}^{2} . \end{matrix}

Innen, mivel

m_{c}

nem lehet 0 (

α = 43^{\circ}

folytán a háromszög nem lapulhat egyenes szakasszá),

\begin{matrix} c^{2} = a^{2} + b^{2} + a b . \end{matrix}

(1)

Másrészt a cosinus-tétel szerint

\begin{matrix} c^{2} = a^{2} + b^{2} - 2 a b cos γ \end{matrix}

A két kifejezést összehasonlítva

cos γ = - \frac{1}{2}

, tehát

γ < 180^{\circ}

miatt

γ = 120^{\circ}

lehet csak és ebben az esetben (1), s így az eredeti összefüggés is valóban teljesül. Ez esetben

α + β = 60^{\circ}

, tehát a háromszög szögei

α = 43^{\circ}

β = 17^{\circ}

γ = 120^{\circ}

II. megoldás: Felhasználva a terület meghatározására szolgáló

2 t = a b sin γ

összefüggést, a 0-tól különböző

a b

-értékkel osztva és négyzetre emelve kapjuk, hogy

\begin{matrix} sin^{2} γ = sin^{2} α + sin^{2} β + sin α sin β, \end{matrix}

(2)

vagy

\begin{matrix} sin^{2} α + sin^{2} β - sin^{2} γ + sin α sin β = 0. \end{matrix}

Alakítsuk át először a középső különbséget, szögfüggvények összegének és különbségének szorzatalakját használva [ehelyett a

sin γ = sin (α + β)

kifejezés tagokra bontásával is célhoz érhetnénk]

\begin{matrix} sin^{2} β - sin^{2} γ = (sin β + sin γ) (sin β - sin γ) = \\ = 2 sin \frac{β + γ}{2} cos \frac{β - γ}{2} \cdot 2 cos \frac{β + γ}{2} sin \frac{β - γ}{2} = \\ = 2 sin \frac{β + γ}{2} cos \frac{β + γ}{2} \cdot 2 sin \frac{β - γ}{2} cos \frac{β - γ}{2} = \\ = sin (β + γ) sin (β - γ) = sin α sin (β - γ) . \end{matrix}

Ezt felhasználva

\begin{matrix} sin^{2} α + sin^{2} β - sin^{2} γ + sin α sin β = sin α [sin α + sin (β - γ)] + sin α sin β = \\ = 2 sin α sin \frac{α + β - γ}{2} cos \frac{α - β + γ}{2} + sin α sin β = \\ = 2 sin α sin \frac{180^{\circ} - 2 γ}{2} cos \frac{180^{\circ} - 2 β}{2} + sin α sin β = \\ = 2 sin α sin (90^{\circ} - γ) \cdot cos (90^{\circ} - β) + sin α sin β = \\ = 2 sin α sin β cos γ + sin α sin β = 2 sin α sin β (cos γ + \frac{1}{2}) . \end{matrix}

E szorzat csak úgy lehet 0, ha

cos γ = - \frac{1}{2}

, azaz

γ = 120^{\circ}

Megjegyzések: 1. A II. megoldásban a lapunk 560. feladalaban (VIII. köt. 82. old.) szereplő

\begin{matrix} sin^{2} α + sin^{2} β - sin^{2} γ = 2 sin α sin β cos γ, ha α + β + γ = 180^{\circ} \end{matrix}

(3)

azonosságot bizonyítottuk be és alkalmaztuk. Többen fel is használták készen ezt az azonosságot a megoldáshoz.
2. Néhányan a (2) összefüggésből jutottak (1)-hez, felhasználva a sinustételt az

\frac{a}{sin α} = \frac{b}{sin β} = \frac{c}{sin γ} = λ

alakban, vagy pontosabban az

a = 2 r sin α

stb. összefüggéseket, ahol

r

a háromszög köré írt kör sugara. Ugyanezen az úton a cosinus-tétel is goniometriai összefüggéssé alakítható, éppen a (3) azonossággá, és (2)-vel összehasonlítva adja a kívánt eredményt.