Kezdőlap


Feladat:	1954. évi Matematika OKTV I. forduló 3. feladata	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1954/május, 132 - 136. oldal		PDF \| MathML
Témakör(ök):	Parabola egyenlete, Egyenesek egyenlete, Téglalapok, Háromszögek egybevágósága, Középvonal, Eltolás, Parabola, mint kúpszelet, OKTV
Hivatkozás(ok):	Feladatok: 1954/május: 1954. évi Matematika OKTV I. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Válasszuk a parabola tengelyét $x$ -tengelynek, csúcsérintőt $y$ -tengelynek, ekkor a parabola egyenlete

\begin{matrix} y^{2} = 2 p x . \end{matrix}

Legyen a parabola

x_{1}

y_{1}

pontja az érintési pont, akkor az érintő egyenlete

\begin{matrix} y y_{1} = p (x + x_{1}), \end{matrix}

ahol

\begin{matrix} y_{1}^{2} = 2 p x_{1}, \end{matrix}

azaz

\begin{matrix} x_{1} = \frac{y_{1}^{2}}{2 p} . \end{matrix}

Így az érintési pontban emelt merőleges, ill. az

F (0, \frac{p}{2})

fókuszból az érintővel párhuzamosan húzott egyenes egyenlete

\begin{matrix} y - y_{1} = - \frac{y_{1}}{p} (x - \frac{y_{1}^{2}}{2 p}) \end{matrix}

azaz

\begin{matrix} 2 p y_{1} x + 2 p^{2} y = y_{1} (y_{1}^{2} + 2 p^{2}) \end{matrix}

illetve

\begin{matrix} y = \frac{p}{y_{1}} (x - \frac{p}{2}), \end{matrix}

azaz

\begin{matrix} 2 p x - 2 y_{1} y = p^{2} . \end{matrix}

Innen kiküszöbölve

y

-t, ill.

x

-et

\begin{matrix} 2 p (y_{1}^{2} + p^{2}) x = y_{1}^{4} + 2 p^{2} y_{1}^{2} + p^{4} = {(y_{1}^{2} + p^{2})}^{2}; 2 (p^{2} + y_{1}^{2}) y = y_{1} (y_{1}^{2} + p^{2}) . \end{matrix}

Oszthatunk

p^{2} + y_{1}^{2}

-tel, mert ez nem lehet 0 és

y_{1}

-et kiküszöbölve kapjuk, hogy

2 y = y_{1}

;

2 p x = y_{1}^{2} + p^{2} = 4 y^{2} + p^{2}

, azaz

y^{2} = \frac{p}{2} (x - \frac{p}{2})

; ez pedig olyan parabola egyenlete, melynek csúcspontja

(0_{1} \frac{p}{2})

, az eredeti parabola fókusza, paramétere pedig az eredeti parabola paraméterének negyedrésze.

\begin{matrix} * \end{matrix}

A feladat megoldható koordináták és (ami lényegében ugyanazt jelentené) Pythagoras tételének felhasználása nélkül is. Ekkor a következő összefüggésekre lesz szükségünk: a parabola tetszés szerinti

P

pontjának a vetülete a direktrixen legyen

Q

, ekkor a

P

pontban húzott érintő az

F P Q ∢

szögfelezője, vagy ami ezzel egyenértékű, a parabola fókuszából az érintőkre bocsátott merőlegesek talppontjainak mértani helye, a parabola csúcsérintője.
Valóban meghúzva az

F P Q ∢

felezőjét (mely merőlegesen metszi

Q F

-et a csúcsérintőre eső

R

felezőpontban), erre

F P = P Q

, de az egyenes bármely más

P'

pontjára

F P' = P' Q

, az utóbbi távolság pedig nagyobb

P'

-nek a direktrixtől mért távolságánál (6. ábra).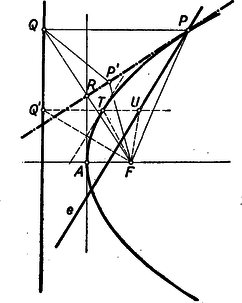

6. ábra

Így az egyenesnek minden

P

-től különböző pontja a direktrixhez közelebb van, mint a fókuszhoz, tehát a parabola ugyanazon oldalára esik. Könnyen látható az is, hogy minden más

P

-n átmenő egyenesnek van pontja a parabolának mindkét oldalán². Így valóban e szögfelező a parabola érintője. Az ábra alapján fordítva is könnyű a csúcsérintő bármely

R

pontjához megkeresni azt a

P

pontot a parabolán, melyben húzott érintőre

F

-ből merőlegest bocsátva annak talppontja, éppen

R

lesz.

II. megoldás: Legyen

P

-ből a direktrixre bocsátott merőleges talppontja

Q

F Q

felezőpontja

R

, az érintőre

P

-ben bocsátott merőleges és az

F

-ből az érintővel húzott párhuzamos metszéspontja

M

(7. ábra).

7. ábra

A segédtétel szerint

F R P ∢ = 90^{\circ}

, tehát az

F M P R

négyszög téglalap, így

M P ♯ F R

, de akkor egyszersmind

M R ∥ P Q

. Bocsássunk

P

-ből merőlegest a parabola tengelyére; messe ez

M R

-t, ill. a tengelyt az

S

, ill.

T

pontban. Ekkor az oldalak párhuzamossága és

M P = F R

miatt,

M P S_{▵} ≅ F R A_{▵}

, s így

P S = R A = \frac{1}{2} P T

M S = F A = \frac{p}{2}

.
Az

M

pontok mértani helye tehát az adott parabolából a következő módon keletkezik: először minden pontnak a parabola tengelyétől való távolságát felére csökkentjük, azután az így keletkezett görbét

\frac{p}{2}

távolsággal eltoljuk. Az utóbbi lépés a görbe alakját nem változtatja meg; az

A

pontot, mely az első lépésnél helyben marad,

F

-be viszi át. Az első lépésnél viszont a parabolából újabb parabola keletkezik, melynek a csúcsa és tengelye azonos az eredeti parabolával, paramétere pedig negyed-akkora. (L. jelen számunkban a 618. sz. feladatot.)

III. megoldás. Az

F M P R

téglalap átlói egyenlők és felezik egymást, így

R N

, mint az

F P Q_{▵}

középvonala párhuzamos

Q P

-vel, vagyis merőleges a csúcsérintőre és

R N = N F

(8. ábra), tehát az

N

pont olyan parabolát ír le, melynek az eredeti parabolával közös a fókusza, direktrixe pedig az eredeti parabola csúcsérintője, tehát paramétere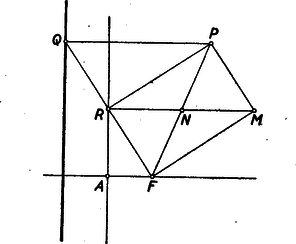

\frac{p}{2}

.³

8. ábra

Minden egyes

N

pontból úgy nyerjük a megfelelő

M

pontot, hogy a csúcsérintőtől való távolságát kétszeresre nyújtjuk. Ezzel ismét parabolát nyerünk, amelynek újra feleződik a paramétere, csúcsa pedig

F

-be kerül.

Megjegyzés: Felhasználtuk, hogy ha egy parabolát a direktrixtől egy irányban kétszeresen megnyújtunk, vagy ha ugyancsak egy irányban a tengelye felé

1 / 2

arányban összehúzzuk, akkor ismét parabolát kapunk, mindkét esetben kisebb paraméterrel: előbbi esetben az eredeti paraméter fele, utóbbi esetben a negyede lesz az új paraméter. Ez azonban semmikép sem magától értetődő, még csak az összes parabolák hasonlóságából sem következik. Legkönnyebb koordináták segítségével belátni. (Mellesleg az első megoldásban

M

koordinátáira adódó

x = \frac{1}{2 p} (y_{1}^{2} + p^{2}) = x_{1} + \frac{p}{2}

y = \frac{y_{1}}{2}

is éppen a II. megoldásban elemien bizonyított összefüggéseket fejezi ki.) A II. és III. megoldásban viszont éppen a koordinátákat akartuk elkerülni, tehát csak akkor mondhatjuk, hogy ez sikerült, ha a föntebb említett tényeket is koordináták és Pythagoras tételének felhasználása nélkül tudjuk bizonyítani. Ez sem ütközik nehézségbe. A III. megoldásra vonatkozóan megmutatjuk, a II. megoldással kapcsolatos bizonyítást ennek alapján az olvasóra bízzuk (l. a 618. feladatot).
Legyen

d

A

és

F

egy parabola direktrixe, csúcsa és fókusza;

P

egy pontja,

Q

annak vetülete

d

-n és legyen

Q P' = 2 Q P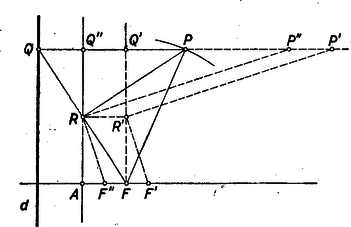

(9. ábra).

9. ábra

Segédtételünk értelmében

Q F

szakasz

R

felezőpontjára

P R F ∢ = 90^{\circ}

és

R

természetesen a csúcsérintőn van. Ha

P'

valóban parabolát ír le, akkor ennek csúcsa az

F

pont kell, hogy legyen. Az ebben

d

-vel párhuzamosan húzott egyenes messe a

P Q

egyenest

Q'

-ben, felezőpontja legyen

R'

. Ismét segédtételünk értelmében elegendő azt megmutatni, hogy az

R'

-ben

P' R'

-re bocsátott merőleges egy a

P'

pont helyzetétől független

F'

pontban metszi az

A F

tengelyt.
Toljuk el

R' P'

-t önmagával párhuzamosan úgy, hogy

R' R

-be kerüljön. Ugyanez az eltolás vigye

F'

-t,

P'

-t, ill.

Q'

-t,

F''

P''

Q''

-be. Mivel

F' F'' = R R' = \frac{p}{2}

, független a

P'

pont helyzetétől, így elegendő azt megmutatni, hogy

F''

helyzete is független. Tudjuk, hogy

\begin{matrix} Q Q'' = R R' = P'' P', amiből Q'' P'' = 2 Q'' P . \end{matrix}

Mivel

\begin{matrix} P R F ∢ = P'' R F'' ∢ = 90^{\circ}, \end{matrix}

így

\begin{matrix} P Q'' R_{▵} \sim R A F_{▵} és P'' Q'' R_{▵} \sim R A F''_{▵}, \end{matrix}

mert megfelelő oldalaik páronként merőlegesek. Így

\begin{matrix} \frac{1}{2} = \frac{P Q''}{P'' Q''} = \frac{P Q''}{Q'' R} \cdot \frac{Q'' R}{Q'' P''} = \frac{R A}{A F} \cdot \frac{A F''}{R A} = \frac{A F''}{A F}, \end{matrix}

azaz

\begin{matrix} A F'' = \frac{1}{2} A F; \end{matrix}

tehát

A F''

és így a vele egyenlő

F F'

is független a

P'

ponttól és fele az eredeti parabola megfelelő adatának.

P'

tehát parabolát ír le, melynek paramétere feleakkora, mint az eredeti paraboláé, és ez volt a bizonyítandó.

²Legyen

e

egy

P R

-től különbözd egyenes

P

-n át. Ennek azon félegyenesének pontjai mely

P

-ből indulva a direktrix és

P R

közti hegyes szögtérbe lép, könnyen láthatóan a fókusztól vannak távolabb, mint a direktrixtől, viszont messe az

F

-ből

e

-re bocsátott merőleges a direktrixet

Q'

-ben. Emeljünk

Q'

-ben a direktrixre merőlegest, messe ez

F Q'

felezőmerőlegesét, illetőleg

e

-t a

T

, ill.

U

pontban, akkor belátható, hogy

T' Q'

és

U

közt van

F T = T Q'

s így

F U < F T + T U = Q' T + T U - Q' U

, vagyis

U

a fókuszhoz van közelebb, mint a direktrixhez, tehát

e

átmetszi a parabolát.

³Úgy is látható ez, hogy az $S$ pontok az eredeti parabolának az $F$ pontból felére kicsinyített képét alkotják.