Feladat: 1954. évi Matematika OKTV I. forduló 2. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1954/május, 131 - 132. oldal  PDF  |  MathML 
Témakör(ök): Párhuzamos szelők tétele, Párhuzamos szelők tételének megfordítása, Középpontos és egyéb hasonlósági transzformációk, Forgatva nyújtás, Körülírt kör, Középponti és kerületi szögek, Húrnégyszögek, Háromszögek hasonlósága, OKTV
Hivatkozás(ok):Feladatok: 1954/május: 1954. évi Matematika OKTV I. forduló 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Készítsünk vázlatot, a középső párhuzamos távolság a másik kettőtől legyen p és q, a középső egyenes messe BC-t a D pontban (a jelöléseket az 1. ábra mutatja). Ekkor nyilván 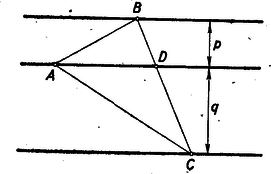BD:DC=p:q.

 
 
1. ábra
 

Ennek alapján a szerkesztés menete: az adott A'B'C' háromszögben megszerkesztjük a B'C'-t p:q arányban osztó D' pontot (2. ábra).
 
 
2. ábra
 

B'-ben és C'-ben párhuzamost húzunk A'D'-vel, már a keresett ábrához hasonlót kapunk. Ezt kell szükség szerint nyújtani, vagy zsugorítani az adott egyeneseknek megfelelően.
Ez például úgy tehető meg, hogy a középső párhuzamos egyenesre rámásoljuk az A'D' távolságot és e fölé mint közös oldal fölé, átmásoljuk a 2. ábrából a p, ill q szélességű síksáv oldalaira az A'D'B', ill. A'D'C' háromszögeket. Így egy az eredetileg megadott háromszöggel egybevágó A'B'C'▵-et nyerünk (3. ábra).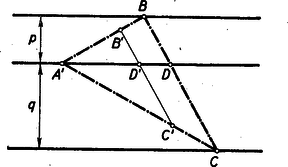
 
 
3. ábra
 

Messe az A'B' oldal a p szélességű síksáv külső szélét B-ben, és húzzunk B-n át B'C'-vel párhuzamost, amely az A'D'-t D-ben, az A'C'-t C-ben metszi. Az így nyert ABC▵ az A'B'C'▵-nek az A' pontból ABA'B' arányban való nagyítása (ill. kicsinyítése) és BDDC=B'D'D'C'=pq miatt a C pont szükségképpen a q szélességű síksáv külső szélén fekszik. Tehát az ABC▵ eleget tesz követelményeinknek.
Tetszés szerint választhatjuk ki, hogy melyik csúcs megfelelője melyik egyenesre essék, tehát 3!=6-féle megoldás lehetséges. Az ezekből tükrözéssel és eltolással keletkező megoldások már mind egybevágóak e 6 háromszög valamelyikével s így nem adnak azoktól lényegesen különböző megoldást.
 

II. megoldás. A B pontot úgy vihetjük át C-be, hogy elforgatjuk A körül a BAC∢=B'A'C'∢= szöggel és közben ACBC=A'C'A'B'=b'c' arányban meg is nyújtjuk, (vagy rövidítjük, A'B'C' legyen az adott háromszög). Mivel e mozgások adatai függetlenek a keresett megoldástól, a feladatot megoldhatjuk forgatva nyújtással.
Válasszunk pl. a középső egyenesen tetszőlegesen egy A pontot és e körül forgassuk el a felső egyenest B'A'C'=α szöggel és egyidejűleg nyújtsuk A-ból A'C':A'B'=b':c' arányban (4. ábra).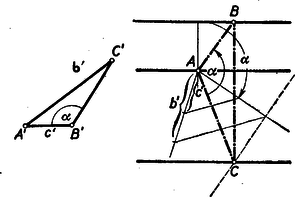
 
 
4. ábra
 

A kapott egyenes messe az alsó párhuzamost C-ben és szerkesszük meg a felső egyenes azon B pontját, mely a forgatva nyújtásnál C-be ment át. Az ABC▵ A-nál lévő szöge és az ezt közrezáró oldalak aránya megegyezik az A'B'C' háromszög megfelelő adataival, tehát valóban hasonló a két háromszög.
 

III. megoldás: Készítsünk vázlatot. Rajzoljuk meg a háromszög köré írt kört, messe ez a középső párhuzamost A-n kívűl még a D pontban. Ekkor a kerületi szögek tétele szerint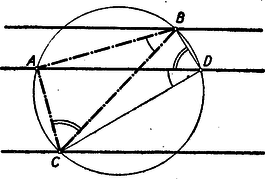
ADB∢=ACB∢ésADC∢=ABC∢.
Ennek alapján a szerkesztés, ha az adott háromszög A'B'C': a középső egyenes tetszés szerinti D pontjában rámérjük ezen egyenes egyik félegyenesének két oldalára az A'C'B', ill. A'B'C' szögeket (5. ábra).
 
 
5. ábra
 

Messék ezek a megfelelő párhuzamos egyenest B-ben, ill. C-ben. Mérjük rá végül BC-re C-ben a B'C'A'∢-et BC ellenkező oldalára mint amelyiken D van. Messe ez a középső párhuzamost A-ban. Az AB távolsága C és D pontokból egyenlő szög alatt látszik, s így ABCD húrnégyszög. Ebből következik, hogy ABC∢=ADC∢=A'B'C'∢, tehát az ABC▵ szögeiben megegyezik az adott A'B'C'▵-gel, s így hasonló hozzá.