Feladat: 1953. évi Matematika OKTV II. forduló 2. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1953/szeptember, 4 - 6. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Középvonal, Egyenlő szárú háromszögek geometriája, Thalesz-kör, Trapézok, Pont körüli forgatás, OKTV
Hivatkozás(ok):Feladatok: 1953/szeptember: 1953. évi Matematika OKTV II. forduló 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ez okozta a legkevesebb nehézséget, bár sokan ágyúval lőttek verébre, amikor trigonometriai és koordinátás számításokat használtak ennek a tisztán I. osztályos anyagismerettel is megoldható feladatnak megoldásához. Itt csak néhányat mutatunk be a számos elemi megoldás közül. Jelöljük a szög csúcsát σ-val és tegyük fel mindig, hogy q≤p. Ezt szimmetria okokból megtehetjük az általánosság csorbítása nélkül. B tehát mindig O és B1 közt van.

 

I. megoldás: Az AOB▵ és B1OA1▵ hasonló, mert O-nál fekvő szögük közös, az ezt közrezáró oldalak pedig az utóbbi háromszögben kétszer akkorák, mint az előbbiben. Bocsássunk másrészt A1-ből merőlegest az OB szárra. Mivel az O-nál lévő szög 60∘, így e merőleges talppontja O-tól 12OA1=q távolságra van, vagyis B-vel azonos. Bocsássunk C-ből is merőlegest OB-re ennek talppontja legyen D. Mivel CD az A1B1B▵ középvonala, azért BD=DB1, vagyis a BCB1▵ egyenlőszárú. Ebből és a fenti hasonlóságból adódik, hogy az 1. ábrán egyformán jelzett szögek egyenlők. Mivel az A1-nél és B1-nél megjelölt szögek összege az O-nál lévő 60∘-os szöget 180∘-ra egészíti ki, azért 60∘-osnak kell lennie az 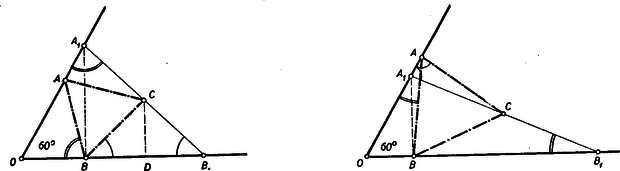ABC∢-nek is.
 
 
1. ábra          2. ábra
 

Ugyanúgy látható, hogy BAC∢=60∘, ha p≤2q, ha azonban 2q<p, akkor az A-nál megjelölt szög (2. ábra) az A1OB1▵ A1-nél lévő külső szögével egyenlő. Viszont ez esetben az egyíves és kétíves szög különbsége adja ki az O-nál lévő 60∘-ot s így egyszersmind BAC∢=60∘. Az ABC▵-nek tehát minden esetben A-nál és B-nél 60∘-os szöge van. Így harmadik szöge is 60∘-os. tehát a háromszög szabályos.
II. megoldás: Az előző megoldásban láttuk, hogy A1B⊥OB1. Hasonlóan következik, hogy B1A⊥OA. Így A és B az A1B1 fölötti Thales körön vannak, melynek középpontja C, tehát AC=BC (3. ábra). Az ACB∢ az AA1B∢=OA1B∢-höz, mint kerületi szöghöz, tartozó középponti szög. Mivel az előbbi szög az O-nál lévő 60∘-os szög pótszöge, azaz 30∘, azért a hozzátartozó középponti szög 60∘-os, tehát az egyenlő szárú ABC▵ egyik szöge 60∘, s így a háromszög szabályos.
Figyeljük meg, hogy a bizonyítás független p és q nagyság viszonyától. Ez állni fog a későbbi megoldásokra is.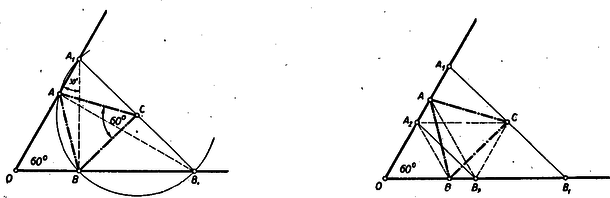
 
 
3. ábra          4. ábra
 

III. megoldás: Jelöljük OA1 ill. OB1 felezőpontját A2-vel ill. B2-vel. Megmutatjuk, hogy az ABC▵ minden oldala egyenlő az A2B2 távolsággal (4. ábra).
OA2=q=OB és OB2=p=OA, tehát OA2B▵ és OAB2▵ szabályosak. Így AA2BB2 egyenlőszárú trapéz, tehát átlói egyenlők: AB=A2B2.
Egyenlőszárú trapéz az A2BB2C négyszög is, mert A2C∥OB1 mint az A1OB1▵ középvonala; B2C e háromszög egy másik középvonala, tehát B2C=12OA1=q=A2B. Így ezen trapéz átlói is egyenlők: BC=A2B2.
Az AA2B2C négyszögről már tudjuk, hogy trapéz, mert B2C középvonal. Az OA2CB2 paralelogrammából és OAB2 szabályos háromszögből A2C=OB2=AB2, tehát a trapéz átlói egyenlők, így a trapéz egyenlő szárú, vagyis AC=A2B2. Az ABC háromszög tehát szabályos.
IV. megoldás: Ha p=q, a kérdéses pontokat jelöljük A∘, A1, B, B1∘, C∘-v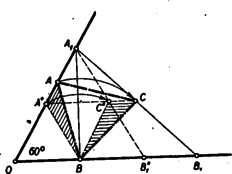al (5. ábra).
 
 
5. ábra
 

Ez esetben az A∘BC∘ háromszöget az OA1B1∘ szabályos háromszög oldalközéppontjai alkotják, tehát szintén szabályos. Növeljük most meg OA∘-t, akkor A∘ valamilyen A helyzetbe kerül, B1∘ egy olyan B1-be, melyre B1∘B1=2A∘A, C pedig az OB-vel párhuzamos A∘C∘ egyenes meghosszabbításán mozdul el és olyan C helyzetbe jut, melyre C∘C=12B1∘B1=A∘A, mert a baloldali távolság, az A1B1∘B1▵ középvonala. Forgassuk az AA∘B▵-et B körül az órajárásával megegyező irányba 60∘-kal. Ekkor A∘ átmegy C∘-ba A∘A iránya párhuzamossá válik OB1-ével s így az éppen megállapított távolságegyenlőségek folytán A éppen C-re kerül. AB és CB tehát 60∘-os elforgatással egymásba vihető, amiből következik, hogy az ABC háromszög szabályos.
Egyszerűbb bizonyításhoz jutunk, ha az egymásba forgatott háromszögekhez hozzácsatoljuk az egybevágó OA∘B ill. A∘BC∘ egybevágó háromszögeket (Ez annak felel meg, hogy az A pontot nem az A∘ helyzetből, hanem az O pontból elindulva mozdítjuk el a végső helyzetébe.)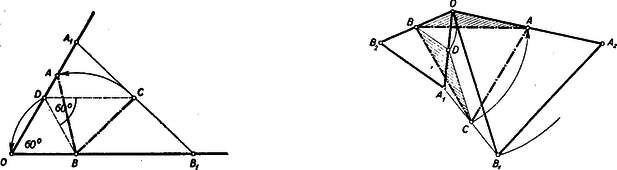
 
V. megoldás: Legyen OA1 felezőpontja D (6. ábra). Ekkor DC az A1OB1▵ középvonala, így DC=12OB1=OA és DC∥OB1. Másrészt OD=12OA1=q=OB, tehát CDB∢=DBO∢=60∘. Forgassuk a BCD háromszöget B körül az óra járásával ellenkező irányba 60∘-kal. Ekkor D éppen O-ba kerül, C pedig a BO-val 60∘-ot bezáró egyenesre, tehát OA1-re, éppen az A pontba. Eszerint BC 60∘-os elforgatással BA-ba megy át, tehát az ABC háromszög szabályos.
 
 
6. ábra          7. ábra
 

Általánosítások: A tétel többféleképpen általánosítható. L. pl. a jelen számban kitűzött 147. sz. gyakorlatot. Egy másik általánosítás a következő: Legyen OA1B2 és A2B1O két szabályos háromszög, melyek O csúcspontja egybeesik és a megadott két körüljárás egyező irányú, akkor az OA2, B2O ill. A1B1 távolságok A, B ill. C felezőpontjai szabályos háromszöget alkotnak. (Versenytételünk ennek az általánosított feladatnak azon speciális esete, amelyben az O csúcsból kiinduló oldalak is egymásra kerülnek, amikor az A1 és B2 csúcsokat említenünk sem kell.)
Ezen állítás éppenúgy bizonyítható, mint az eredeti verseny feladat. Vegyük pl. az V. megoldás mintájára az OA1 szakasz D felezőpontját (7. ábra), akkor a BCD▵-et 60∘-kal elforgatva a D pont O-ba a DC szakasz pedig OA-ra kerül, tehát BC 60∘-os elforgatással átvihető BA-ba, s így az ABC háromszög szabályos.
Az állítás így minden esetre elég körülményesen hangzik, ezzel szemben messzemenően általánosítható. Nem lényeges benne sem a háromszögek szabályossága, csak a hasonlóságuk, sem a közös csúcspont, és a felezőpont is mással pótolható. Így pl. igaz az 554. sz. feladatban bizonyításra kitűzött tétel.