Kezdőlap


Feladat:	1952. évi Matematika OKTV II. forduló 1. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Dömölki Bálint , Fehér János , Kántor Sándor , Keresztély Sándor
Füzet:	1952/szeptember, 8 - 10. oldal		PDF \| MathML
Témakör(ök):	Kör geometriája, Szögfelező egyenes, Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Tengelyes tükrözés, Szinusztétel alkalmazása, Kör (és részhalmaza), mint mértani hely, OKTV
Hivatkozás(ok):	Feladatok: 1952/szeptember: 1952. évi Matematika OKTV II. forduló 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A $C$ pont rajta van azon az Apollonius-féle körön, melynek minden $P$ pontjára nézve $\frac{P B}{P A} = \frac{1}{2, 6} = \frac{5}{13}$ . A $B A C ∢$ akkor maximális, ha $A P$ a kör érintője. Ez az érintési pont lesz tehát a keresett $C$ pont. Kimutatjuk, hogy $C B A ∢$ derékszög.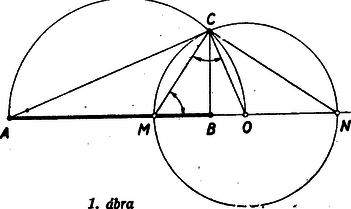

Az Apollonius-féle kör középpontját

O

-val és az

A B

egyenessel való metszéspontjait

M

és

N

-nel jelölve (1. ábra), a

C M

egyenes az

A B C_{▵}

A B

oldalát

\frac{M B}{M A} = \frac{5}{13} = \frac{C B}{C A}

arányban metszi, mert

M

is a kör egy pontja. Ebből viszont következik, bogy

C M

A C B ∢

felezője,

\begin{matrix} A C M ∢ + M C O ∢ = 90^{\circ}, \end{matrix}

(1)

mert az érintő merőleges a körsugárra.
Láttuk, hogy

A C M ∢ = M C B ∢

. Másrészt a

C O M

egyenlőszárú háromszögből

\begin{matrix} M C O ∢ = O M C ∢ . \end{matrix}

Helyettesítsük az (1) alatti egyenlőségben szereplő szögeket a velük egyenlő szögekkel

\begin{matrix} M C B ∢ + O M C ∢ = 90^{\circ}, \end{matrix}

de akkor az

M B C ▵

harmadik szöge,

M B C ∢

90^{\circ}

, vagyis az

A B C ▵

derékszögű és így

A B = \sqrt[]{A C^{2} - B C^{2}} = B C \sqrt[]{2, 6^{2} - 1} = B C \sqrt[]{5, 76} = 2, 4 B C

, vagyis

\begin{matrix} B C = \frac{5}{12} A B . \end{matrix}

Tehát a

C

pontot a

B

pontban

A B

-re emelt merőleges egyenesen kell elhelyezni

B

-től

\frac{5}{12} \cdot A B

távolságban.

II. megoldás: Képzeljük a feladatot megoldottnak és alkalmazzuk az

A B C ▵

-re a sinus-tételt;

\begin{matrix} \frac{sin α}{sin β} = \frac{C B}{C A} = \frac{5}{13} \end{matrix}

amiből

\begin{matrix} sin α = \frac{5}{13} \cdot sin β . \end{matrix}

Mivel

α

szükségképpen hegyesszög, azért

α

akkor maximális, ha

sin α

maximális;

sin α

pedig akkor veszi fel a legnagyobb értéket, ha

sin β = 1

, vagyis

β = 90^{\circ}

III. megoldás: Tekintsünk egy

C_{1}

pontot, melyre nézve

\frac{C_{1} B}{C_{1} A} = \frac{1}{2, 6} = \frac{5}{13}

és

C_{1} B A ∢

hegyes, továbbá egy

C_{2}

pontot, melyre nézve

\frac{C_{2} A}{C_{2} B}

értéke ugyancsak

\frac{5}{13}

, de a

C_{2} B A ∢

tompa. Legyen

C_{1} C'_{1}

ill.

C_{2} C'_{2}

, a

C_{1}

ill.

C_{2}

pontoknak távolsága az

A B

egyenestől (2. ábra) és az

A

-nál keletkező szögeket jelöljük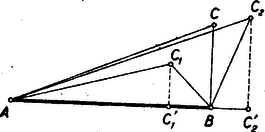

α_{1}

ill.

α_{2}

-vel.

2. ábra

Mivel

C_{1} C'_{1} < C_{1} B

és

C_{2} C'_{2} < C_{2} B

, azért

\begin{matrix} sin α_{1} = \frac{C C_{1}}{C_{1} A} < \frac{C_{1} B}{C_{1} A} = \frac{5}{13} és sin α_{2} = \frac{C_{2} C'_{2}}{C_{2} B} < \frac{C_{2} B}{C_{2} A} = \frac{5}{13} . \end{matrix}

Tehát az

A

-nál levő szög sinusa mindig kisebb

\frac{5}{13}

-nál, kivéve, ha a

C B A ∢

derékszög, ekkor

sin α = \frac{C B}{C A} = \frac{5}{13}

, vagyis ez esetben

sin α

és vele együtt

α

maximális.
Így oldotta meg a feladatot Fehér János (Győr, Révai gimn.)

IV. megoldás: Mindazon közös

A B

oldalú

A B C

háromszögekben, melyekre teljesül az

A C : B C = 2, 6

kikötés, a

C

-nél fekvő szög felezője az

A B

oldalt olyan

M

pontban metszi, melyre

A M : B M = A C : B C = 2, 6

. Az

M

pont helyzete független a háromszög alakjától. Tükrözzük a

C M B

háromszöget a

C M

szögfelezőre. A

B

pont tükörképe

B'

A C

háromszögoldalra esik és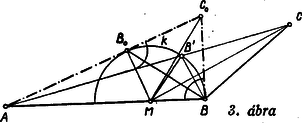

\begin{matrix} M B' = M B \end{matrix}

C

pont helyzetétől független távolság. Az összes ilyen pontok tehát az

M

középpontú és

B

-n átmenő

k

körön sorakoznak. (3. ábra).

Megfordítva, ha

B'

ennek a körnek tetszés szerinti pontja, akkor messük el az

A B'

egyenest a

B M B' ∢

felezőjével. Az így keletkező

A B C

háromszögben

M C

szögfelező, mert

M B'

tükörképe

M C

-re

M B

, a

C

ponté pedig önmaga, tehát a

C B'

oldalegyenes tükörképe

C B

. Ebből következik az is, hogy

\begin{matrix} A C : B C = A M : B M = 2, 6, \end{matrix}

tehát az

A B C ▵

megfelel a követelményeknek.
Az eredeti feladat tehát helyettesíthető azzal, hogy a

k

kör mely

B_{0}

-ját kell

A

-val összekötni, hogy a keletkező

B_{0} A B ∢

a lehető legnagyobb legyen. Ez a

B_{0}

nyilván az

A

-ból húzható érintő érintési pontja. Ez esetben

\begin{matrix} M B_{0} ⊥ A B_{0} \end{matrix}

Szerkesszük meg a fent leírt módon az ezen

B_{0}

ponthoz tartozó

A B C_{0}

háromszöget. Ebben is

M B C_{0} ▵

M B_{0} C_{0} ▵

tükörképe, s így

\begin{matrix} A B C_{0} ∢ = M B_{0} C_{0} ∢ = 90^{\circ} . \end{matrix}

V. megoldás: Keressük azon közös

A B

oldalú

A B C

háromszögek közül, melyekre

A C : B C = 2, 6

azt, amelyben a

B A C ∢

a lehető legnagyobb. A szögek azonban nem változnak, ha a háromszögeket nagyítjuk, vagy kicsinyítjük. Így helyettesíthetjük az összes háromszöget olyanokkal, melyekben az

A C

oldal közös. Ekkor

\begin{matrix} B C = \frac{A C}{2, 6} = \frac{5}{13} A C \end{matrix}

is az összes háromszögekben egyenlő, az összes

B

pontok tehát egy

C

körül

r = \frac{5}{13} \cdot A C

sugárral rajzolt körön vannak. A

B A C ∢

akkor maximális, ha

A B

e kör érintője, tehát

B C ⊥ A B

és Pythagoras-tétele alapján

\begin{matrix} A B = 2, 4 B C, vagyis B C = \frac{5}{12} \cdot A B . \end{matrix}

Számosan differenciálással oldották meg a feladatot, ami ‐ mint láttuk ‐ teljesen felesleges.