Kezdőlap


Feladat:	1952. évi Matematika OKTV I. forduló 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1952/szeptember, 6 - 8. oldal		PDF \| MathML
Témakör(ök):	Szögfüggvények, síkgeometriai számítások, Egyenlő szárú háromszögek geometriája, Derékszögű háromszögek geometriája, Háromszögek hasonlósága, OKTV
Hivatkozás(ok):	Feladatok: 1952/szeptember: 1952. évi Matematika OKTV I. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A betűzést az ábra mutatja.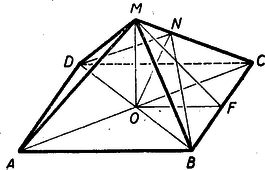

Legyen az alapnégyzet egy oldala

B C = a

, az alapnégyzet félátlója

O B = O C = \frac{a \sqrt[]{2}}{2}

. A keresett

O M

-et jelöljük

m

-mel. A

B D

átlón át az

M C

oldalélre merőleges sík messe az oldalélt

N

-ben. Tehát

O N ⊥ M C

.
A feltétel szerint a

B N D ∢ = 120^{\circ}

. Legyen

O C N ∢ = α

. Mivel a

B N D

egyenlőszárú háromszögben a szárakkal szembenfekvő szögek

30^{\circ}

-osak, azért

\begin{matrix} sin α = \frac{O N}{O C} = \frac{O N}{O B} = tg O B N ∢ = tg 30^{\circ} = \frac{1}{\sqrt[]{3}} . \end{matrix}

Ezt felhasználva, az

O C M

derékszögű háromszögből

\begin{matrix} m = O C \cdot tg α = O C \cdot \frac{sin α}{\sqrt[]{1 - sin^{2} α}} = \frac{a \sqrt[]{2}}{2} \cdot \frac{1 / \sqrt[]{3}}{\sqrt[]{1 - 1 / 3}} = \frac{a \sqrt[]{2}}{2 \sqrt[]{2}} = \frac{a}{2} . \end{matrix}

Jelen esetben

a = 26

cm és így

m = 13

cm.
A keletkező számos derékszögű háromszög sokféle lehetőséget ad arra is a versenyzők ezeket ki is aknázták ‐ hogy trigonometria felhasználása nélkül számítsuk ki a magasságot. Egy ilyen pl. a következő.

II. megoldás:

B F = O F = \frac{a}{2}

. A

B O N ▵

-ből

B N = \frac{B O}{sin 60^{\circ}} = \frac{a \sqrt[]{2}}{2} / \frac{\sqrt[]{3}}{2} = \frac{a \sqrt[]{2}}{\sqrt[]{3}} = \frac{a \sqrt[]{6}}{3} .

M F C

és a

B N C

derékszögű háromszögek hasonlók, mert a

C

-nél fekvő hegyes szögük közös, tehát

\begin{matrix} \frac{M F}{M C} = \frac{B N}{a} = \frac{\sqrt[]{6}}{3}, \end{matrix}

vagyis

\begin{matrix} \frac{M F^{2}}{M C^{2}} = \frac{m^{2} + \frac{a^{2}}{4}}{m^{2} + \frac{a^{2}}{2}} = \frac{2}{3}, \end{matrix}

amiből

\begin{matrix} 3 m^{2} + \frac{3 a^{2}}{4} = 2 m^{2} + a^{2}, \\ m^{2} = \frac{a^{2}}{4}, és így m = \frac{a}{2} . \end{matrix}

III. megoldás: Legyen

M C = b

és

B N = p

. Mivel a feladat szerint

B N O ∢ = 60^{\circ}

, azért

O N = \frac{p}{2}

.
A

C O M ▵

kétszeres területe kétféleképpen állítható elő:

\begin{matrix} 2 t = b \cdot \frac{p}{2} = \frac{a}{2} \sqrt[]{2} \cdot m, \\ vagyis b p = a m \sqrt[]{2} . & (1) \end{matrix}

B C M ▵

kétszeres területe hasonlóképpen

\begin{matrix} b p = a \sqrt[]{m^{2} + \frac{a^{2}}{4}} . \end{matrix}

(1) és (2)-ből következik, hogy

\begin{matrix} a m \sqrt[]{2} = a \sqrt[]{m^{2} + \frac{a^{2}}{4}}, \\ 2 m^{2} = m^{2} + \frac{a^{2}}{4}, \end{matrix}

amiből

\begin{matrix} m = \sqrt[]{\frac{a^{2}}{4}} = \frac{a}{2} . \end{matrix}

IV. megoldás: Vegyünk

6

, a feltételeknek megfelelő, gúlát és helyezzünk először hármat egymás mellé úgy, hogy csúcsaik és egy oldalélük egybeessenek. Mivel az oldallapok szöge

120^{\circ}

és

3

ilyen lapszög került egymás mellé, a

3

gúla hézag nélkül összeillik. Két-két gúla szomszédos oldallapjai pedig

360^{\circ} - 2 \cdot 120^{\circ} = 120^{\circ}

-os szöget fognak alkotni. Így a szomszédos gúlák közé egy-egy újabb gúlát illesztve úgy, hogy ezek csúcsa is összeessék a már összeillesztett gúlák közös csúcsával, zárt testet kapunk, melyet

6

négyzet (a

6

gúla alaplapja) határol. Ez a test tehát csak kocka lehet. Két csúccsal szembefordított gúla magasságainak összege egyenlő a kocka élével, vagyis a gúla alapélével. Ebből következik, hogy a gúla magassága az alapél hosszának felével egyenlő.

Így oldotta meg a feladatot Szabó László (Aszód, Petőfi g. IV. o. t.) és Tuska Ferenc (Cegléd, Kossuth g. IV. o. t.)
A pályázók legnagyobb része trigonometriai táblákkal szögeket határozott meg, ami ‐ mint a fenti megoldások matatják ‐ teljesen felesleges.