Kezdőlap


Feladat:	1952. évi Matematika OKTV I. forduló 1. feladata	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1952/szeptember, 3 - 5. oldal		PDF \| MathML
Témakör(ök):	Kör egyenlete, Hiperbola egyenlete, Egyenesek egyenlete, Hiperbola, mint kúpszelet, OKTV
Hivatkozás(ok):	Feladatok: 1952/szeptember: 1952. évi Matematika OKTV I. forduló 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A körnek az egyenesekkel való metszéspontjai szimmetrikusak a pontból az egyenesekre bocsátott merőlegesekre nézve, tehát célszerű az utóbbi két egyenest koordináta-tengelynek választani, az adott pont lesz tehát az origó. Legyen a ,,függőleges'' egyenes távolsága az $Y$ tengelytől $u$ , a ,,vízszintesé'' az $X$ -tengelytől $v$ ( $u$ és $v$ előjellel veendők). A kör sugara $r$ nyilván nem legkisebb sem $| u |$ sem $| v |$ -nél. Az $r$ sugarú kör által létesített $4$ metszéspont: $(x_{1}, v),$ $(- x_{1}, v)$ , $(u, y_{1})$ , $(u, - y_{1})$ és e metszéspontokban emelt merőlegesek metszéspontjainak koordinátái: $(x_{1}, y_{1})$ , $(- x_{1}, y_{1})$ , $(x_{1}, - y_{1})$ , $(- x_{1}, - y_{1})$ . Az előbbi $4$ pont rajta van az origó körül húzott $r$ sugarú körön, tehát koordinátái kielégítik a következő két egyenletet:

\begin{matrix} x_{1}^{2} + v^{2} = r^{2} \end{matrix}

(1)

és

\begin{matrix} u^{2} + y_{1}^{2} = r^{2} \end{matrix}

(2)

r

-et kiküszöböljük az által, hogy pl. (1)-ből kivonjuk (2)-t, az

\begin{matrix} x_{1}^{2} - y_{1}^{2} + v^{2} - u^{2} = 0, \end{matrix}

vagyis

\begin{matrix} x_{1}^{2} - y_{1}^{2} = u^{2} - v^{2} \end{matrix}

egyenletet kapjuk. Az indexet most már elhagyva annak hangsúlyozására, hogy ha

r

változik az

x_{1}

és

y_{1}

, értékek is változnak és feltéve, hogy

u^{2} \neq v^{2}

\begin{matrix} \frac{x^{2}}{u^{2} - v^{2}} - \frac{y^{2}}{u^{2} - v^{2}} = 0, \end{matrix}

| u | = | v |

; akkor az egyenlet így alakul:

\begin{matrix} x^{2} - y^{2} = (x - y) (x + y) = 0. \end{matrix}

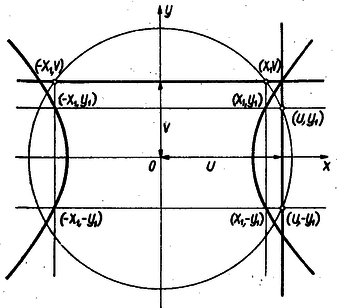Az előbbi egyenlő oldalú hiperbola egyenlete, melynek aszimptotái a koordináta-tengelyek szögfelező egyenesei, az utóbbi egyenletet viszont éppen e két szögfelező pontjainak koordinátái elégítik ki. A

r

változtatásával nyert

(x, y)

pontok mindig kielégítik az első, ill. a második egyenletet, a szerint, hogy milyen

u

és

v

értéke.
Fordítva, ha egy

(x_{0}, y_{0})

pontra nézve

x_{0}^{2} - y_{0}^{2} = u^{2} - v^{2}

(vagyis az

x_{0}

y_{0}

pont rajta van a fenti vonalon), akkor e pontból az adott egyenesekre bocsátott merőlegesek talppontjai:

(x_{0}, v)

és

(u, y_{0})

. Ezek távolsága az origótól:

\sqrt[]{x_{0}^{2} + v^{2}}

és

\sqrt[]{u^{2} + y_{0}^{2}}

a fenti egyenlőség szerint egyenlő, tehát e talppontok rajta vannak az origó körül rajzolt

\begin{matrix} r = \sqrt[]{x_{0}^{2} + v^{2}} = \sqrt[]{u^{2} + y_{0}^{2}} \end{matrix}

sugarú körön, vagyis az

(x_{0}, y_{0})

pont kielégíti a mértani hely feltételeit.
Ezek szerint, ha

| u | \neq | v |

, akkor a mértani hely egyenlő oldalú hiperbola, melynek középpontja az adott pont, tengelyei párhuzamosak az adott egyenesekkel, a tengelyek hosszának fele

\sqrt[]{u^{2} - v^{2}}

. A hiperbola átmegy az adott egyenesek

(u, v)

metszéspontján.
Ha

| u | = | v |

vagyis az adott pont speciálisan a két adott egyenes egyik szögfelezőjén van, akkor a mértani hely a kérdéses szögfelezőből és az adott ponton át rá merőlegesen húzott egyenesből áll. Azt szoktuk mondani, hogy a hiperbola ebben az esetben két egyenesre fajul.

Megjegyzés: Ha az adott egyeneseket választjuk a koordinátarendszer tengelyeinek és az adott pont:

O (u, v)

akkor a geometriai hely egyenlete:

\begin{matrix} \frac{{(x - u)}^{2}}{u^{2} - v^{2}} - \frac{{(y - v)}^{2}}{u^{2} - v^{2}} = 1 \end{matrix}

alakú lesz.