| Feladat: | 14. fizika mérési feladat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Balogh Illés Gyula , Emri Miklós , Furó István , Korcsmár Tamás , Kucsera Gábor , Nálhi Tamás , Szabó László , Wéber Tamás | ||
| Füzet: | 1978/május, 236 - 238. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Mechanikai mérés, Egyéb folyadék- és gázáramlás, Folytonossági (kontinuitási) egyenlet, Folyadékhozam, Mérési feladat | ||
| Hivatkozás(ok): | Feladatok: 1978/január: 14. fizika mérési feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Határozzuk meg a szabadon eső vízsugár alakját! Tegyük fel, hogy a víz belső súrlódásának, felületi feszültségének, a csapszáj és a víz közötti súrlódásnak a hatása figyelmen kívül hagyható! Mivel a víz belső súrlódását elhanyagoltuk, feltehetjük, hogy a víz az keresztmetszetű függőleges cső minden pontján azonos kezdősebességgel hagyja el a csövet, és az esés folyamán a sebességeloszlás minden vízszintes keresztmetszetben homogén marad. Ekkor ‐ a vizet összenyomhatatlannak tekintve ‐ a vízsugár bármely keresztmetszetén idő alatt áthaladó víz mennyisége egyenlő a csapból idő alatt kifolyt víz mennyiségével:
az energia megmaradásából számolható (csak a gravitációs tér hatását vesszük figyelembe):
Ez a képlet csak a fenti feltételek teljesülése esetén írja le helyesen a vízsugár alakját. A kifolyó vízsugár felülete egy darabig sima, majd fodrozódni kezd, cseppekre bomlik. A jelenség kialakulásában a turbulens áramlás játszik lényeges szerepet. A vízsugár alakját a csőszájhoz közel lényegesen befolyásolja a fém és a víz közötti tapadási feszültség hatása. Ez a jelenség kevésbé lényeges, ha a cső falvastagsága lényegesen kisebb, mint annak sugara. A szokásos csapoknál ez nincs így, ezért a vízsugár ‐ főleg kis kifolyási sebesség mellett ‐ szélesebb, mint képletünk alapján várható lenne. A (3) összefüggés a csővégtől a fodrozódás kezdetéig tekinthető jó közelítésnek. Ezen a szakaszon az áramlás nagyjából stabil és a nehézségi erő hatására létrejövő szűkülés jellemzi. 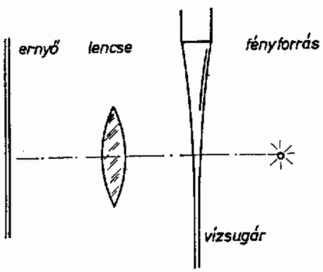 1. ábra A (3) képlet igazolásához szükség van még ismeretére is. Ezt a legegyszerűbben valamely ismert () térfogatú mérőedény megtöltéséhez szükséges idő mérésével végezhetjük el, ugyanis állandó kiömlési sebességet feltételezve:
A kísérlet elvégzését nagy mértékben zavarhatják a vízvezetékben fellépő nyomásváltozások, melyek megváltoztatják a kiömlési sebességet és módosíthatják az áramlás jellegét. Ez a zavaró körülmény kiküszöbölhető, ha a vizet egy olyan tartályból folyatjuk ki, melyben a vízszint változása elhanyagolható. Nálhi Tamás (Nagykáta, Damjanich J. Gimn., III. o. t.) megoldása igen szellemes. Egy megtöltött kádba vékony gumicsövet eresztett, majd a csövet megszíva egyenletesen áramlott át a víz a csövön. Az átáramló víz mennyiségét egy szorító bilinccsel tudta szabályozni. A kifolyt vizet folyamatosan lehet pótolni, csak arra kell ügyelni, hogy ezzel csak kis mértékben zavarjuk meg a kádban kialakult áramlást. Hasonló elven működő tartályt készített Wéber Tamás (Kazincbarcika, Ságvári E. Gimn., IV. o. t.) is. Versenyzőink nagy része a vízsugár átmérőjét közvetett úton mérte ‐ lefényképezte, ill. árnyékát lerajzolta ‐, s az így nyert ,,felvételt'' értékelte ki. Többen próbálkoztak közvetlen méréssel is, pl. tolómérővel vagy sablonok segítségével. Szellemes, habár elég pontatlan módon mérte a vízsugár átmérőjét Emri Miklós (Kazincbarcika, Ságvári E. Gimn., IV. o. t.), aki finom szövésű szitát, ill. Furó István (Nagykanizsa, Landler J. Gimn., IV. o. t.), aki lisztes élű kést húzott el vízszintesen a vízsugár alatt. A szita szálai közt vízhártya maradt ott, ahol a víz átment, míg a késről a vízsugár vastagságának megfelelő szakaszon mosta le a lisztet a víz. Mindkét módszer a valódinál nagyobb átmérőt ad. Néhány megoldónk a feladatot félreértve a teljesen turbulens áramlási szakaszt mérte. A feladat első részét ‐ a vízsugár átmérőjének mérését ‐ legtöbb versenyzőnk jól oldotta meg. A feladat második részét ‐ a mérési eredmények összehasonlítását a 913. feladat alapján számítható eredménnyel ‐ már csak hárman végezték el. Ezeket fogadtuk el teljes értékű megoldásnak. Korcsmár Tamás (Nagykanizsa, Landler J. Gimn., III. o. t.) mérési adatait és a (3) képlet igazolásához szükséges értékeket tüntettük fel a következő táblázatban. 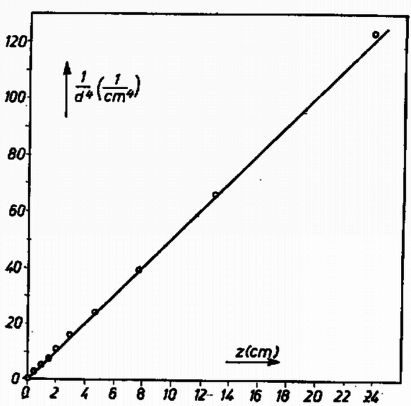 2. ábra A (3) egyenlet szerint, ha |