Kezdőlap


Feladat:	1. fizika mérési feladat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Bányász István , Csekő Gábor , Emvi Miklós , Kovács Zsolt , Nalhi Tamás , Szabó András , Szabolics Imre , Vankó Péter , Zanati Beáta
Füzet:	1976/december, 238 - 240. oldal		PDF \| MathML
Témakör(ök):	Mechanikai mérés, Modern fizikai mérés, Egyéb felületi feszültség, Egyéb folyadékok és gázok egyensúlya, Mérési feladat
Hivatkozás(ok):	Feladatok: 1976/szeptember: 1. fizika mérési feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat szerint az olajfolt átmérőjét kellett meghatározni az olaj mennyiségének függvényében. Egyes megoldók megelégedtek azzal, hogy a mennyiséget csepp egységben adták meg, azonban a különböző dolgozatok összehasonlíthatósága érdekében célszerű meghatározni a csepp tömegét vagy térfogatát.

Zanati Beáta szemcseppentővel csepegtette az olajat. Egy edénybe 100 csepp olajat cseppentett és megmérte az edény tömegét olajjal és üresen:

az üres edény tömege

3, 85

100 csepp olajjal

5, 21

amiből egy csepp olaj tömege

0, 014

g. A tömegmérés hibája kicsi (

0, 01

g), azaz az olajcsepp átlagos tömegét

1 %

-nál pontosabban határozta meg. Természetesen ez nem jelenti azt, hogy az egyes cseppek között ennél nagyobb eltérés nem lehet.
A cseppek átlagos tömege természetesen függ a cseppentőtől és az olajtól is. Szabó András szintén

0, 014

g-os csepptömeget mért, de Bányász István és Csekő Gábor

0, 020

g-os átlagos tömeget kapott. Szabolics Imre a cseppek térfogatára

0, 022 {cm}^{3}

értéket kapott.
Az olajfolt átmérőjének meghatározását Nalhi Tamás mérései alapján mutatjuk be. Az olajat pipettával cseppentette, és minden mérést háromszor végzett el. A mérés eredményeit a következő táblázat tünteti fel:

\begin{matrix} Cseppek száma & 1 & 2 & 5 & 10 & 20 & 50 \\ d_{1}(cm) & 0, 5 & 0, 8 & 1, 2 & 1, 6 & 2, 3 & 3, 8 \\ d_{2}(cm) & 0, 4 & 0, 8 & 1, 1 & 1, 4 & 2, 1 & 3, 5 \\ d_{3}(cm) & 0, 5 & 0, 8 & 1, 2 & 1, 5 & 2, 1 & 3, 6 \\ d_{átlag}(cm) & 0, 47 & 0, 8 & 1, 17 & 1, 5 & 2, 17 & 3, 63 \end{matrix}

Látható, hogy az azonos számú cseppből alkotott olajfoltok átmérői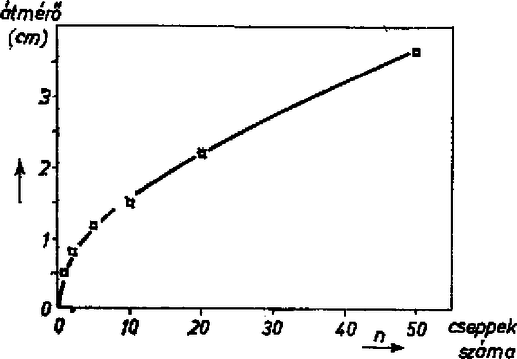

10 %

-os pontossággal megegyeznek. Az átmérő‐cseppek száma összefüggést az 1. ábra mutatja.

1. ábra

A görbe egy vízszintes tengelyű parabolához hasonlít. A megsejtett parabolikus összefüggésről úgy győződhetünk meg, hogy az átmérőket a cseppszám négyzetgyökének függvényében ábrázoljuk (2. ábra).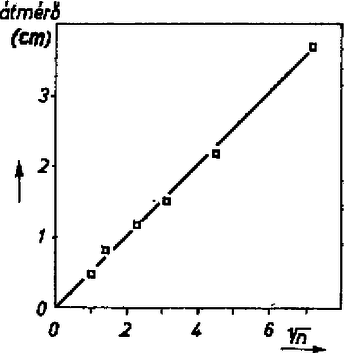

2. ábra

Mivel ebben a koordináta-rendszerben a másodfokú függvény egyenest ad, megállapíthatjuk, hogy az összefüggés a mérési pontosságon belül valóban négyzetgyökös. A keresett kísérleti kapcsolat

\begin{matrix} d = d_{0} \cdot n, \end{matrix}

ahol az illesztett egyenes meredekségéből

d_{0} = 0, 51

cm adódik (

n

a cseppek száma).
Vankó Péter megmutatta, hogyha közvetlenül a cseppentés után mérünk, akkor a folt átmérője

n^{1 / 3}

-nal arányos és később folyik szét annyira a folt, hogy

n^{1 / 2}

-enes összefüggést mérhetünk.
Érdemes megjegyezni, hogy a folt átmérője a tömegén kívül erősen függ a víz szennyezettségétől is. Néhány megoldó ezért desztillált vizet használt. Vigyáznunk kell, hogy a zsíroldó anyagokkal (mosogatópor, mosópor) szennyezett vízen az olajfolt teljesen szétfolyik, a mérést nem lehet elvégezni.
A négyzetgyökös összefüggést azzal magyarázhatjuk, hogy a folt vastagsága

(h)

állandó. A

v = 0, 022 {cm}^{3}

térfogatú cseppet számolva a

h \cdot d^{2} π / 4 = v \cdot n

egyenletből

\begin{matrix} h = \frac{4 v}{π d_{0}} = 0, 55 mm . \end{matrix}