Kezdőlap


Feladat:	Pontversenyen kívüli P.385	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Hraskó András
Füzet:	1984/szeptember, 257 - 258. oldal		PDF \| MathML
Témakör(ök):	Beírt alakzatok, Geometriai egyenlőtlenségek, Terület, felszín, Számtani-mértani egyenlőtlenségek, Szögfüggvények, síkgeometriai számítások, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1983/november: Pontversenyen kívüli P.385

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Bizonyításunkban minden egyenlőtlenség a számtani és a mértani közép közti egyenlőtlenségből következik.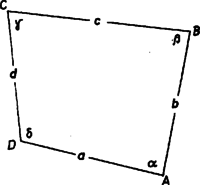

1. ábra

Az 1. ábrán látható jelölésekkel a négyszög területe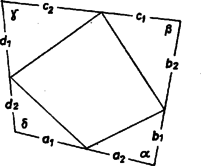

\begin{matrix} 1 = \frac{1}{2} a b sin α + \frac{1}{2} c d sin γ = \frac{1}{2} b c sin β + \frac{1}{2} d a sin δ . \end{matrix}

Így

\begin{matrix} 1 & = \frac{a b sin α + c d sin γ + b c sin β + d a sin δ}{4} \geq \\ ≧ \sqrt[4]{a^{2} b^{2} c^{2} d^{2} sin α sin β sin γ sin δ} = \\ = \sqrt[4]{{(a_{1} + a_{2})}^{2} {(b_{1} + b_{2})}^{2} {(c_{1} + c_{2})}^{2} {(d_{1} + d_{2})}^{2} sin α sin β sin γ sin δ} ≧ \\ ≧ \sqrt[4]{4 a_{1} a_{2} \cdot 4 b_{1} b_{2} \cdot 4 c_{1} c_{2} \cdot 4 d_{1} d_{2} \cdot sin α sin β sin γ sin δ} = \\ = 8 \cdot \sqrt[4]{(\frac{1}{2} a_{2} b_{1} sin α) (\frac{1}{2} b_{2} c_{1} sin β) (\frac{1}{2} c_{2} d_{1} sin γ) (\frac{1}{2} d_{2} a_{1} sin δ)} . \end{matrix}

2. ábra

A 2. ábra szerint a gyökjel alatt álló tényezők mindegyike a levágott kis háromszögek közös

T

területével egyenlő, tehát

1 ≧ 8 T

, azaz

4 T ≦ 1 / 2

. Ebből a feladat állítása azonnal adódik.

Megjegyzés. Az egyenlőség a megoldás szerint csak

a_{1} = a_{2}

b_{1} = b_{2}

c_{1} = c_{2}

és

d_{1} = d_{2}

esetben állhat fönn. Ekkor viszont, mivel a csúcsoknál keletkező háromszögek egyenlő területűek, magasságaik is egyenlők. A négy négyszög szemközti oldalfelező pontjai egyenlő távolságra vannak a másik két oldaltól, tehát a négyszög szemközti oldalai párhuzamosak. Megfordítva, egységnyi területű paralelogramma oldalfelező pontjai által meghatározott négyszög területe

1 / 2

, egyenlőség csak ebben az esetben áll.