Kezdőlap


Feladat:	Pontversenyen kívüli P.367	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Törőcsik Jenő
Füzet:	1983/november, 148 - 150. oldal		PDF \| MathML
Témakör(ök):	Lefedések, Logikai feladatok, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1982/október: Pontversenyen kívüli P.367

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az egység oldalú négyzet lefedhető 9 kisebb, egyenként 1/3 oldalú négyzettel. Egy kis négyzet átlója $\sqrt[]{2} / 3 < 0, 5$ , tehát bármely két pontjának távolsága kisebb 1/2-nél. Következésképp egy kis négyzetbe legfeljebb egy pontot helyezhetünk el ‐ így az egész egységnégyzetbe legfeljebb 9 pontot.
Másrészt 8 pont elhelyezhető a kívánalmaknak megfelelően (1. ábra).

1. ábra

Így maximálisan 8 vagy 9 pontot tudunk úgy elhelyezni az egységnégyzetben, hogy bármely kettő távolsága 1/2-nél nagyobb legyen.

Törőcsik Jenő (Bp., Fazekas M. Gyak. Gimn., IV. o. t.)

Megjegyzés. Megmutatjuk, hogy a pontos felső korlát 8. Ehhez tegyük fel, hogy mégis sikerült elhelyeznünk 9 pontot a követelményeknek megfelelően ‐ ebből fogunk ellentmondásra jutni.

Tekintsünk egy tetszőleges

a_{n}

monoton csökkenő, 0-hoz tartozó sorozatot. Minden

n

-re rajzoljunk az egységnégyzet oldalai és középvonalai mentén

a_{n}

szélességű sávokat (2. ábra).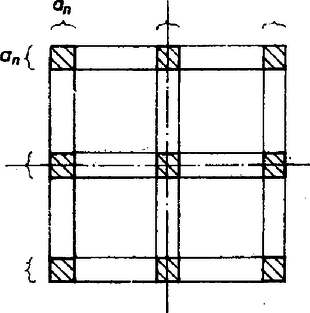

2. ábra

Ezek 9 darab

a_{n} \times a_{n}

méretű négyzetet vágnak ki a nagy négyzetből. Ha sikerül úgy megadnunk az

{a_{n}}

sorozatot, hogy minden

n

-re a kis négyzetek mindegyikébe a 9 pont közül egy essen, akkor készen vagyunk:

{lim}_{}^{} a_{n} = 0

miatt a kiválasztott pontok csak a négyzet csúcsai, oldalfelező pontjai és középpontja lehetnek ‐ ellentétben azzal, hogy közülük nem bármely kettő távolsága nagyobb 1/2-nél.

Az maradt hátra, hogy megadjunk egy megfelelő

{a_{n}}

sorozatot.

a_{1} = 1 / 3

nyilván jó: az egységnégyzetet 9 kisebb négyzetre osztjuk, s az előbb láttuk, hogy ezek mindegyikébe pontosan egy pontnak kell kerülnie.
Tegyük fel, hogy valamely

a_{n} \leq 1 / 3

-ra már tudjuk, hogy a pontok a 2. ábra megfelelő részeibe esnek. Legyen

A B C D

és

A' B' C' D'

két "szomszédos''

a_{n} \times a_{n}

-es kis négyzet (3. ábra), a köztük levő távolság

C B' = D A' = (1 - 3 a_{n},) / 2

3. ábra

A 9 pont közül egy‐egy esik az

A B C D

, ill.

A' B' C' D'

négyzetekbe. E két pont közti távolság nagyobb 1/2-nél. Ezért például az

A B C D

négyzetben levő pont nem lehet a

C D

oldalhoz

P C = Q D = a_{n} / 10

-nél közelebb. Ugyanis ha felveszünk egy tetszőleges pontot a

P C D Q

téglalapban, annak az

A' B' C' D'

négyzet tetszőleges pontjától ‐ így az abban levő kiválasztott ponttól is ‐ való távolsága legfeljebb

\begin{matrix} P D' = \sqrt[]{P Q^{2} + Q D'^{2}} = \\ = \sqrt[]{a_{n}^{2} + {(\frac{a_{n}}{10} + \frac{1 - 3 a_{n}}{2} + a_{n})}^{2}} = \\ = \sqrt[]{\frac{1}{4} - \frac{2}{5} a_{n} (1 - 2, 9 a_{n})} \end{matrix}

ami

0 < a_{n} \leq 1 / 3

miatt kisebb 1/2-nél.
Ha kivágjuk a 2. ábra négyzeteiből az összes ily módon kapott "tiltott'' téglalapot, a 9 pontnak a megmaradt részekbe kell esniük (4. ábra).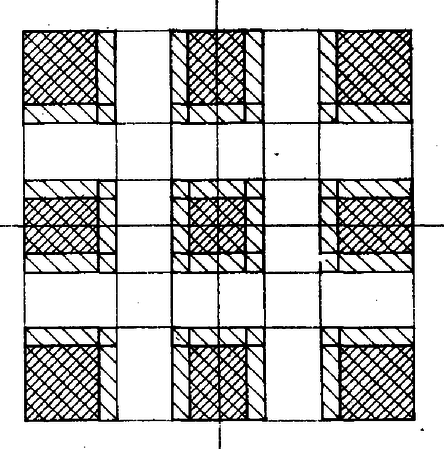

4. ábra

Ezeket a részeket viszont ‐ mint az könnyen látható ‐ lefedik az

a_{n + 1} = 0, 9

a_{n}

-hez tartozó

a_{n + 1} \times a_{n + 1}

-es kis négyzetek. Tehát ezek mindegyikébe is pontosan egy esik a megadott pontok közül.
Az

a_{1} = 1 / 3

a_{n + 1} = 0, 9

a_{n}

formulával definiált sorozat tehát jó, találtunk egy megfelelő

{a_{n}}

sorozatot. Ezzel az állítást is igazoltuk.