| Feladat: | Pontversenyen kívüli P.360 | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Borsó Zsolt , Törőcsik Jenő | ||
| Füzet: | 1982/december, 211 - 214. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Középpontos és egyéb hasonlósági transzformációk, Pontversenyen kívüli probléma | ||
| Hivatkozás(ok): | Feladatok: 1982/március: Pontversenyen kívüli P.360 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Az állítást 8 lépésben bizonyítjuk. Egy tetszőleges alakzatnak a fenti transzformáció szerinti képét a rövidség kedvéért -vel jelöljük. 1. Ha a síknak kölcsönösen egyértelmű ponttranszformációja, és pedig a sík két tetszőleges alakzata, akkor és alakzatának pontosan annyi közös pontja lesz, mint az és alakzatoknak van. Két nem metsző (párhuzamos) egyenes szerinti képe tehát két nem metsző alakzat lesz. Ha a transzformációról még azt is tudjuk, hogy egyenest egyenesbe visz, akkor párhuzamos egyenespár képe párhuzamos egyenespár. 2. Nyilvánvaló az is, hogy kölcsönösen egyértelmű ponttranszformáció alakzatok közös pontját a képalakzatok közös pontjába viszi, tehát egyenesek metszéspontjának a képe a képegyenesek metszéspontja. A paralelogramma párhuzamos oldalegyeneseit egy kölcsönösen egyértelmű, egyenestartó ponttranszformáció párhuzamos oldalegyenesekbe, a csúcsokat (nem párhuzamos oldalegyenesek metszéspontjait) a képegyenesek metszéspontjaiba viszi, tehát paralelogramma képe paralelogramma. 3. Érintse most az egyenes a kört. Ha a transzformáció kört körbe visz, akkor az egyenes érinteni fogja a kört, tehát kört érintő egyenest a képkört érintő egyenesbe visz. 4. Ha a körön kívül fekszik, akkor -ből húzható érintőegyenes -hoz. Ezért a -ből húzott egyenes is érinteni fogja a kört, tehát a körön kívül lesz. Így a kör külső pontjai a képkör külső pontjaiba, a körvonal pontjai a képkörvonal pontjaiba, a kör belső pontjainak képei a képkör belső pontjaiba mennek át. Húzzunk kört az szakasz mint átmérő fölé. Az egyenesnek a körön belül levő pontjai lesznek az szakasz belső pontjai, így a transzformáció ezeket a pontokat a képkör belső pontjaiba viszi, vagyis az szakasz belső pontjaiba. Azt kaptuk, hogy az szakasz pontjainak képei az szakasz pontjainak képei lesznek. A 2. és 4. pont alatt mondottakból már következik, hogy ha a szakasz az szakasz párhuzamos eltolásával keletkezik, akkor ugyanez áll a képszakaszokra is: a szakasz az szakasz eltolásával keletkezik. (Az négyszög ugyanis pontosan akkor paralelogramma, ha a szakasz az szakasz párhuzamos eltoltja.) 5. Most belátjuk, hogy a transzformáció kör átellenes pontjait a képkör átellenes pontjaiba viszi. Legyen ugyanis és a kör két átellenes pontja. Érintse az egyenes a kört az pontban, az egyenes pedig a pontban. Ekkor az és egyenesek is érinteni fogják a kört. Másrészt párhuzamos -fel, mert a kört átellenes pontokban érinti e két egyenes. Következésképp is párhuzamos -vel. Tehát és átellenes pontokban érinti a kört. De ez a két érintési pont éppen és , ill. és közös pontjának a képe, vagyis és képe. és képe tehát valóban a képkör két átellenes pontja. 6. Húzzunk egyenest a kör középpontján keresztül. Ez az egyenes a kört két átellenes pontjában metszi, tehát az egyenes képe a kört két átellenes pontban metszi, vagyis átmegy a kör középpontján. Húzzunk még egy egyenest a kör középpontján keresztül. Ennek képe is átmegy középpontján. A két egyenes metszéspontjának a képe a képegyenesek metszéspontja, tehát a kör középpontja éppen a kör középpontja lesz. Vagyis a transzformáció bármely kör középpontját a képkör középpontjába viszi. Ezt az állítást így is fogalmazhatjuk: ha az szakasz az elforgatásával keletkezik, akkor ugyanez áll a képszakaszokra: a szakasz elforgatottja. ( és pontosan akkor van ugyanazon az középpontú körön, ha az elforgatottja.) 7. Ha két szakasz egyenlő, akkor egy párhuzamos eltolással és egy elforgatással átvihető az egyik a másikba. Láttuk, hogy egy szakasz eltolásának a képsíkon is a képszakasz valamilyen párhuzamos eltolása, elforgatásának a képszakasz valamilyen elforgatása felel meg. Ebből következik, hogy egyenlő hosszú szakaszok képei egyenlő hosszú szakaszok. 8. Ha az szakaszt egyenlő részre osztjuk, akkor az osztópontok képei a képszakaszt egyenlő részre bontják, hiszen egyenlő hosszú szakaszok képei egyenlő hosszúak. Ha most az és szakaszok aránya racionális; mondjuk , akkor az szakasz elosztható , a szakasz egyenlő részre úgy, hogy a szomszédos osztópontok közti szakaszok a két szakaszon egyenlő hosszúak. A transzformáció egyenlő szakaszokat egyenlő hosszú darabokba visz, tehát az és szakasz képei is feloszthatók ugyanúgy , ill. egyenlő részre. Tehát . A feladat állítása ebből már következik: ha az háromszög oldalainak aránya , akkor ugyanez igaz az arányra is. II. megoldás. Legyen kölcsönösen egyértelmű egyenes- és körtartó ponttranszformáció. Azt állítjuk, hogy egymást metsző ill. érintő egyenlő sugarú körök szerinti képei egymást metsző ill. érintő egyenlő sugarú körök lesznek. Vegyünk fel ugyanis 5 kört a következőképpen, legyen négy egyenlő sugarú kör, menjen mind a négy keresztül ugyanazon az ponton, a és körök érintsék egymást, az és a körök szintén, végül az ötödik, kör középpontja legyen , és érintse ez a kör , , , , mindegyikét. Az érintési pontokat rendre jelöli. ( sugara a többi kör átmérőjével egyenlő, lásd az ábrát.) 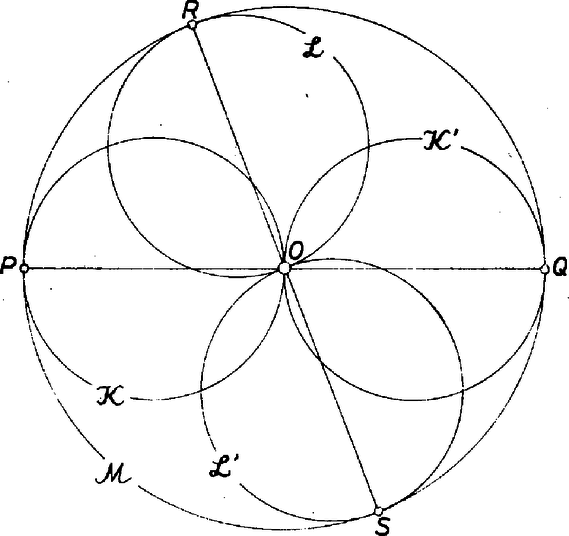 egyenestartó, így az egyenesre illeszkedő , , pontok. , , képei is egy egyenesre illeszkednek. A páronként egymást érintő , , körök 3 érintési pontja tehát egy egyenesen van. Ismeretes, hogy ha 3 egymást páronként (különböző pontban) érintő kör 3 érintési pontja egy egyenesen van, akkor mindhárom kör középpontja is ezen az egyenesen van, s ez az egyenes mindhárom körből átmérőt metsz ki. Ezt az állítást felhasználva azt kapjuk, hogy az kör középpontja rajta van a , , pontok meghatározta egyenesen és ill. a , ill. kör átmérője. Szimmetrikus okoskodással adódik, hogy az kör középpontja rajta van az , , pontok meghatározta egyenesen, és ill. az ill. kör átmérője. Vagyis a és egyenesek metszéspontja. De ezek metszéspontja éppen , vagyis éppen az kör középpontja. Következésképp az , , , szakaszok az kör sugarai, s egyenlők. Másrészt e szakaszok a , , , körök átmérői, azaz ezek a körök egyenlő sugarúak. Beláttuk tehát, hogy egy ponton keresztülmenő, egyenlő sugarú körök képe egy ponton keresztülmenő egyenlő sugarú körök, továbbá érintő körpár képe érintő körpár. Legyen most az háromszög oldalainak aránya . Osszuk fel az oldalt a pontokkal három, a oldalt az pontokkal négy, a oldalt a pontokkal öt egyenlő részre. Rajzoljuk meg az , , , , , , , , , , , átmérőjű köröket. Ez a 12 kör mind egyenlő sugarú, és mindegyiknek van közös pontja az előtte, ill. utána említettel (az utolsónak az elsővel is), s ha ez a közös pont nem az csúcsok egyike, akkor a körök érintik egymást. A fent bizonyított dőlt betűs állítás szerint e 12 pontból és 12 körből álló alakzat szerinti képe egy hasonló alakzat lesz, mert egyenlő sugarú körök egyenlő sugarú körökbe, érintőkörök érintőkörökbe, metsző körök metsző körökbe és metszés-, ill. érintési pontok metszés-, ill. érintési pontba mennek át. Ezzel beláttuk, hogy az háromszög oldalainak az aránya lesz. Borsó Zsolt (Budapest, Fazekas M. Gyak. Gimn., III. o. t.) A sík kölcsönösen egyértelmű transzformációja pontosan akkor hasonlóság, ha egyenest egyenesbe és kört körbe visz. 2. A II. megoldásból tulajdonképpen azt kapjuk, hogy ha egy háromszög oldalainak aránya , és egészek, akkor ugyanez a háromszög képének oldalaira is áll. Ebből még közvetlenül nem következik, hogy bármely két szakasz képe egyenlő. (A bizonyításban nem szerepel az a lépés, hogy párhuzamos szakaszok képe párhuzamos lesz.) folytonosságát kihasználva azonban már ennyiből is következik, hogy hasonlóság. |