Feladat: Pontversenyen kívüli P.342 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bali János ,  Csere Kálmán 
Füzet: 1981/november, 146 - 150. oldal  PDF  |  MathML 
Témakör(ök): Sakktáblával kapcsolatos feladatok, Pontversenyen kívüli probléma, Gráfelmélet
Hivatkozás(ok):Feladatok: 1980/december: Pontversenyen kívüli P.342

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Számozzuk meg az oszlopokat és a sorokat, és ha egy bábu az i-edik oszlopban (vagy sorban) áll, akkor mondjuk azt, hogy ez a bábu lefogja az i-edik oszlopot (vagy sort). 8 bábut kell kiválasztanunk úgy, hogy minden sort és minden oszlopot pontosan egy bábu fogjon le. Ezt 8 lépésben tesszük. A k-adik lépésben (k=1,2,...,8) az első k sorból választunk ki egy-egy bábut úgy, hogy azok összesen k oszlopot fogjanak le. Így a 8. lépésben 8 olyan bábuhoz jutunk, amelyek közt minden sorból és minden oszlopból is egy bábu szerepel.
Az 1. lépésben az 1. sor egy tetszőleges bábuját kiválasztjuk.
A k. lépésben tegyük fel, hogy 2≤k≤8 és a (k-1)-edik lépésben már kiválasztottunk az első k-1 sorból egy-egy bábut úgy, hogy a kiválasztott k-1 bábu összesen k-1 oszlopot fog le.

 

1. ESET: Ha a le nem fogott oszlopok valamelyikének k-adik sorában áll bábu, akkor a k-adik lépésben ezt a bábut (vagy ha több ilyen van, egyet tetszőlegesen ezek közül) és a (k-1)-edik lépésben kiválasztott k-1 bábut választjuk. Így kiválasztottunk egy-egy bábut az első k sorból úgy, hogy a k kiválasztott bábu k oszlopot fog le.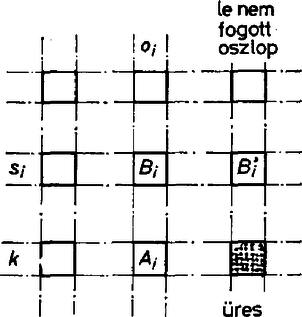
 

1. ábra
 

2. ESET: Ha a le nem fogott oszlopok egyikének k-adik sorában sem áll bábu, akkor a k-adik sorban álló 4 bábu mindegyike olyan oszlopban áll, amelyet a k-1 bábu lefog. Legyenek a k-adik sorban álló bábuk A1, A2, A3, A4, oszlopszámaik legyenek rendre O1, O2, O3, O4. Az Oi-edik oszlopot lefogó bábu legyen Bi, Bi sorának sorszáma legyen Si(i=1, 2, 3, 4). B1, B2, B3, B4 a (k-1)-edik lépésben kiválasztott k-1 bábu közül való, így az Si-k 1 és k-1 közé esnek. Minthogy az Ai-k különbözők, azért a Bi-k is különböznek. Másrészt a (k-1)-edik lépésben egy sorból csak egy bábut választottunk, így az Si-k is mind különbözők. Tekintsük most valamelyik olyan oszlopot, amelyet a k-1 kiválasztott bábu nem fog le. (Ilyen oszlop van.) A feltétel szerint ebben is 4 bábu áll, másrészt a k-adik sorában esetszétválasztásunknak megfelelően nem áll bábu. A 4 bábunak tehát a fennmaradó 7 sorban kell állnia, így az S1, S2, S3, S4 sorok valamelyikében kell állnia bábunak. Mondjuk az Si-edik sorban áll bábu, ez a bábu B'i. A (k-1)-edik lépésben kiválasztott bábuk közül most kihagyjuk Bi-t és hozzáválasztjuk Ai-t és B'i-t (1. ábra). Így az első k sorból egy-egy bábut választottunk ki, és ez a k bábu lefogja az összes, a (k-1)-edik lépésben lefogott oszlopot, valamint egy új oszlopot, összesen tehát k oszlopot. Ezzel a k-adik lépést, és az állítás bizonyítását is befejeztük.
 

Csere Kálmán (Veszprém, Lovassy L. Gimn., IV. o. t.)

 

II. megoldás. Szemléltessük az oszlopokat és a sorokat egy-egy ponttal, az i-edik oszlopot az Oi pont, a j-edik sort az Sj pont képviselje (2. ábr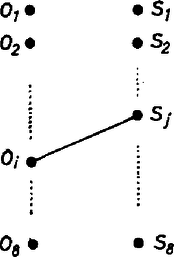a).
 

2. ábra
 

Ha az i-edik oszlop j-edik sorában áll bábu, akkor kössük össze egy szakasszal az Oi és Sj pontokat. Így olyan alakzathoz jutunk, ahol minden pontból pontosan 4 szakasz indul ki, hiszen minden sorban és minden oszlopban pontosan 4 bábu áll. Továbbá semelyik két Oi pont nincs összekötve és semelyik két Sj pont sincs összekötve. Ezt az alakzatot (gráfot) jelöljük G-vel.
A G gráf minden OiSj szakasza egy-egy bábunak felel meg a sakktáblán. Ki kell választanunk 8 olyan bábut a táblán, hogy minden sorból és minden oszlopból pontosan egy bábu legyen kiválasztva. Ez a gráfban azt jelenti, hogy ki kell választani 8 olyan OiSj szakaszt, hogy minden Oi és minden Sj pont pontosan egy kiválasztott szakasznak legyen a végpontja (3. ábr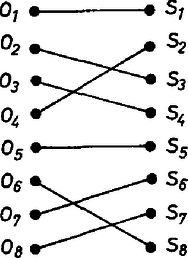a).
 

3. ábra
 

A feladat állítása tehát így fogalmazható át: ha a G gráfban minden Oi és Sj pontból 4-4 szakasz indul ki, Oi pontok csak Sj pontokkal, Sj pontok csak Oi pontokkal vannak összekötve, akkor van a gráfban 8 olyan OiSj alakú szakasz, hogy minden O-pont és minden S-pont pontosan egy kiválasztott szakasznak a végpontja.
Ezt az állítást fogjuk most bebizonyítani.
A G gráfból készítünk egy új gráfot, amelynek kétszer annyi pontja lesz, és minden pontból pontosan két szakasz fog kiindulni. Húzzunk szét minden Oi pontot két ponttá: a két új pont legyen O'i; és O''i. Az Oi-ból kiinduló 4 szakaszt osszuk szét a két új pont között, kettő O'i-ből, kettő O''i-ből induljon az új gráfban. Húzzuk ugyanígy szét az Sj-pontokat is, és osszuk kétfelé a belőlük induló szakaszokat is! (4. ábra).
 

4. ábra
 

Így kapunk egy G' gráfot, ahol 16 darab O'i és O''i alakú pont (röviden: O-pont) és 16 darab S'j és S''j alakú pont (röviden: S-pont) van. Minden O- és S-pontból két-két szakasz indul ki, O-pontok csak S-pontokkal, S-pontok csak O-pontokkal vannak összekötve.
Az olyan zárt törtvonalat, amelynek csúcsai O-pontok vagy S-pontok, és ahol a csúcsokat a gráfban szereplő szakaszok kötik össze, a gráf "körének'' nevezzük (5. ábr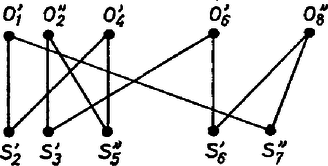a).
 

5. ábra
 

A törtvonal persze metszheti magát az O- és S-pontoktól különböző pontokban, ezeket azonban nem tekintjük csúcsoknak. Minthogy G' gráfunkban minden pontból pontosan két szakasz indul ki, nyilvánvalóan ilyen "körökre'' bomlik úgy, hogy semelyik két "körnek'' nincsen közös csúcsa, és a "körök'' együttesen a gráf összes szakaszát lefedik (egyrétűen).
Egyetlen ilyen "körben'' sem lehet két szomszédos O-pont vagy két szomszédos S-pont, így minden "körnek'' páros sok csúcsa és páros sok szakasza van. Minden egyes "kör'' csúcsokat összekötő szakaszai kiszínezhetők tehát felváltva piros és kék színnel. Így minden csúcsból egy piros és egy kék szakasz indul ki.
A G' gráf szakaszai megszínezhetők tehát piros és kék színnel úgy, hogy minden O-pontból és minden S-pontból pontosan egy piros színű él és pontosan egy kék színű él indul ki. (A piros élek is, a kék élek is a 3. ábráéhoz hasonló alakzatot képeznek, csak nem 16, hanem 32 ponton).
Keressük meg a piros szakaszok megfelelőit a G gráfban és színezzük ki őket pirossal. A ki nem színezett szakaszokat dobjuk ki G-ből. Így egy G0 gráfhoz jutunk. Minden Oi pontnak két O-pont, és minden Sj pontnak két S-pont felel meg G'-ben, másrészt G'-ben minden O-pontból és minden S-pontból pontosan egy piros szakasz indul ki, így G0-ban minden Oi és Sj pontból pontosan két-két szakasz indul ki. G0-ban is igaz, hogy Oi alakú pontból csak Sj alakú pontba megy szakasz, Sj alakúból pedig csak Oi alakúba. A G'-re alkalmazott gondolatmenet tehát G0-ra is alkalmazható: G0 szakaszai is átszínezhetők két színnel, mondjuk feketével és fehérrel úgy, hogy minden Oi és Sj pontból pontosan egy fekete és egy fehér szakasz induljon ki. Így a fekete szakaszok külön, és a fehér szakaszok külön is 8 olyan OiSj szakaszt adnak, amilyet keresünk. Minthogy G0 szakaszai G-nek is szakaszai, dőlt betűs állításunkat, és ezzel a feladat állítását is, bebizonyítottuk.
 

Bali János (Budapest, Fazekas M. Gyak. Gimn., IV. o. t.)
 

Megjegyzések. 1. Az I. megoldás gondolatmenete könnyen kiterjeszthető a következő általános állítás bizonyítására is: Egy 2n×2n-es sakktáblára 2n2 bábut helyeztünk el úgy, hogy minden sorban és minden oszlopban pontosan n bábu álljon. Ekkor kiválasztható 2n darab bábu úgy, hogy minden oszlopból és minden sorból pontosan egy bábu legyen kiválasztva.
2. A II. megoldás gondolatmenete egy másik általánosítás bizonyítását adja: Egy n×n-es sakktáblára 4n bábut helyeztünk el úgy, hogy minden sorban és minden oszlopban pontosan 4 bábu álljon. Ekkor kiválasztható n bábu úgy, hogy minden oszlopból és minden sorból pontosan egy bábu legyen kiválasztva.
3. A II. megoldás valójában még ennél is többet mond: azt mondja, hogy kiválasztható n bábu a kívánt tulajdonsággal, majd a maradó bábukból kiválasztható még egyszer n bábu a kívánt tulajdonsággal. (Nemcsak a fekete, hanem a fehér élek is megfelelnek céljainkra.) Ha most még meggondoljuk, hogy G' kék éleinek megfelelőire is ugyanez a gondolatmenet alkalmazható, akkor azt kapjuk, hogy a 32 szakasz (32 bábu) felbontható 8+8+8+8 szakaszra (bábura) úgy, hogy mindegyik 8 szakasz (bábu) külön-külön megfelel a feltételeknek. Általában pedig a következő állítást kapjuk: Egy n×n-es sakktáblára 4n bábut helyeztünk el úgy, hogy minden sorban és minden oszlopban pontosan 4 bábu álljon. Ekkor a 4n bábu 4 darab n-es csoportba osztható úgy, hogy egy-egy csoport n bábuja minden sorból és minden oszlopból pontosan egy bábut tartalmazzon.
4. Igaz (de nehezebben bizonyítható) az 1., 2., és 3. megjegyzésben kimondott állítások következő közös általánosítása:
Egy n×n-es sakktáblára kn bábut helyeztünk el úgy, hogy minden sorban és minden oszlopban pontosan k bábu álljon. Ekkor a k⋅n bábu k db n-es csoportba osztható úgy, hogy egy-egy csoport n bábuja minden sorból és minden oszlopból pontosan egy bábut tartalmazzon.
5. Ha egy gráf csúcsai két osztályba sorolhatók úgy, hogy egy osztályon belüli csúcsok nincsenek szakasszal összekötve, akkor a gráfot páros gráfnak nevezzük. A II. megoldásban csupa páros gráf szerepel (a két osztály mindig az O-pontok és az S-pontok osztálya volt). Láttuk a megoldás folyamán, hogy egy páros gráf minden "körének'' páros sok csúcsa van (innen ered nevük is).
Ha egy gráfban vannak olyan, a csúcsokat összekötő szakaszok, amelyek közül a gráf minden csúcsa pontosan egynek a végpontja, akkor ezeket a szakaszokat együtt a gráf 1-faktorának nevezzük (3. ábra). A II. megoldás során bizonyított (dőltbetűs) állítás tehát a következő formában mondható ki:
Ha egy páros gráf két osztályában 8-8 (vagy áltálában n-n) csúcs van, minden csúcsból 4 szakasz indul ki, akkor a gráfban van 1-faktor. Az is igaz, hogy a gráfban szereplő 32 (általános esetben 4n) szakasz 4 darab 1-faktorra bontható.
Belátható az is (de nehezebben bizonyítható), hogy ez az állítás 4 helyett tetszőleges k-ra is igaz.
Ha egy páros gráf két osztályában n-n csúcs van, minden csúcsból k szakasz indul ki, akkor a gráfban van 1-faktor is, és a gráfban szereplő k⋅n szakasz k darab 1-faktorra bontható.
Ez az állítás ekvivalens a 4. megjegyzés állításával.
6. A II. megoldás egyik lépéseként a G gráfból szakaszok elhagyásával előállítottunk egy olyan G0 gráfot, amelyben minden csúcsból pontosan két szakasz indul ki. Ha most csak az elhagyott szakaszokat tekintjük, ezek is egy olyan G1 gráfot alkotnak, amelyben minden csúcsból két szakasz indul ki (hiszen összesen minden csúcsból 4 szakasz indult ki). Vagyis igaz a következő állítás:
Ha egy páros gráf minden csúcsából pontosan 4 szakasz indul ki, akkor a gráf felbontható két olyan gráfra, amelyek mindegyikében két-két szakasz indul ki minden csúcsból.
Ez az állítás azonban nemcsak páros gráfokra, hanem tetszőleges gráfokra igaz.
Általában igaz a következő:
Ha egy gráfban minden csúcsból pontosan 2k szakasz indul ki, akkor a gráf felbontható a G1,...,Gk gráfokra úgy, hogy minden egyes Gi-ben minden csúcsból pontosan 2 szakasz indul ki.
7. A legtöbb megoldó beleesett abba a tévedésbe, hogy 32 bábut a 8×8-as sakktáblán csak egyféleképpen lehet úgy elhelyezni, hogy minden sorban és minden oszlopban pontosan 4 bábu álljon. Ez nem igaz, amint azt a 6. ábra is mutatja.
 

6. ábra