Feladat: Pontversenyen kívüli P.339 Korcsoport: 18- Nehézségi fok: nehéz
Füzet: 1981/december, 216 - 218. oldal  PDF  |  MathML 
Témakör(ök): Egyéb sokszögek geometriája, Pontversenyen kívüli probléma, Síkgeometriai bizonyítások, Ponthalmazok
Hivatkozás(ok):Feladatok: 1980/október: Pontversenyen kívüli P.339

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen T az önmagát nem metsző zárt töröttvonal. Tekintsük a T által határolt S sokszög minden a oldalához azt az F(a) félsíkot, amelyet T-nek az a oldalegyenese határol, és amely az S sokszögnek az a oldalszakasz felezőpontjához "közeli'' belső pontjait tartalmazza. Jelölje továbbá Fd(a) azt a félsíkot, amely tartalmazza F(a)-t és amelynek a-val párhuzamos határegyenese d távolságra van az a oldalegyenestől (1. ábra).

 

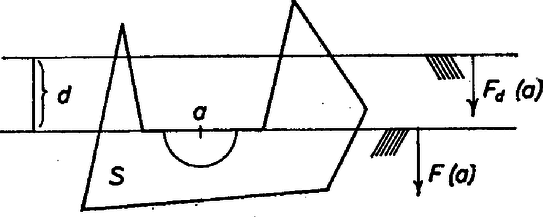1. ábra
 

1. Először azt látjuk be, hogy ha a,b,c három tetszőleges oldala T-nek és d tetszőleges pozitív távolság, akkor az Fd(a),Fd(b),Fd(c) félsíkoknak van közös pontja. Legyen az A'A'' oldalszakasz felezőpontja A0. S zárt sokszög, így van olyan r, hogy az A0 középpontú, r sugarú K kör teljesen tartalmazza S-et (r≧A'A''/2). A K körnek és az Fd(a) egyenesnek két metszéspontja legyen D és E, a DA' és A''E egyenesek metszéspontja legyen G. Ha r-et elég nagyra választjuk, elérhető, hogy DE>A'A'' legyen, s ekkor G az F(a) félsíkba esik (2. ábra).
 

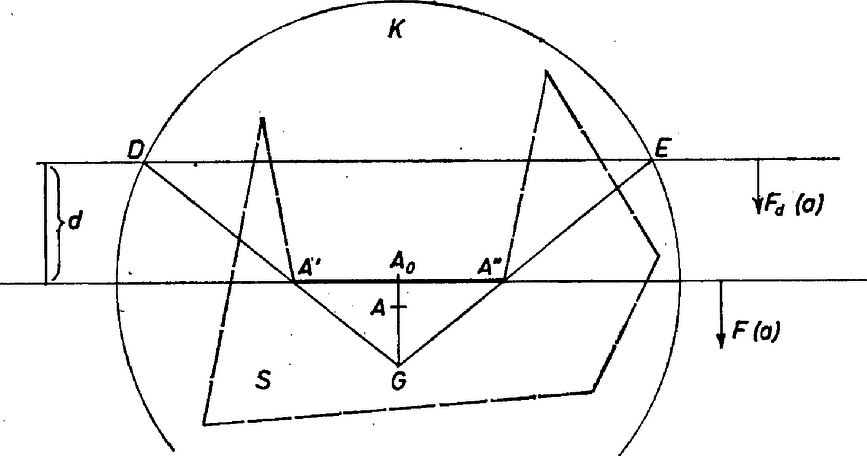2. ábra
 

F(a) definíciója szerint az A0G szakasz belsejében van olyan A pont, amely S-hez tartozik.
Másrészt ha a P pont az S-ben van és a PA szakasz nem metszi az A'A'' oldalt, akkor P az Fa(a) félsíkban is benne van. Ugyanis ekkor P vagy a DGE szögtartományon belül van, vagy az A'A''G háromszögben. Mivel P még S-nek is pontja, ezért a K kör belsejében is benne van, s ez bizonyítja állításunkat. A tehát olyan pont, hogy minden olyan S-beli P pont, amelyre PA nem metszi az A'A'' oldalt, feltétlenül az Fd(a) félsíkban van. Ugyanígy található egy B (ill. C) pont, hogy minden S-beli P pont, amelyre PB (ill. PC) nem metszi a b=B'B'' ill. c=C'C'', oldalszakaszt, az Fd(b) ill. Fd(c) félsíkban van. Az A, B, C pontok S-ben vannak, a feladat feltétele szerint van olyan P pont, amelyre PA, PB, PC szakaszok is S-ben vannak. P tehát S-ben van és PA nem metszi az a , PB nem metszi a b, PC nem metszi a c oldalt. Következésképp P közös pontja az Fd(a), Fd(b), Fd(c) félsíkoknak, ahogyan állítottuk.
2. Most azt bizonyítjuk, hogy F(a), F(b), F(c)-nek is van közös pontja. Ha ez nem így volna, akkor vagy volna köztük kettő, mondjuk F(a) és F(b), amelyek nem metszik egymást (ekkor az a és b oldalegyenes párhuzamos), vagy az a, b, c oldalegyenesek közül bármely kettő metszi egymást, és a metszéspontok által határolt EFG háromszögbe a három félsík egyikének sem esik pontja. Mindkét esetben megválasztható volna d úgy, hogy az Fd(a), Fd(b), Fd(c) félsíkoknak ne legyen közös pontjuk: az első esetben d az a és b egyenesek távolsága harmadának választható; a második esetben d az EFG háromszög legkisebb magassága felének. Így ellentmondásra jutottunk az 1.-ben bizonyított állítással.
Beláttuk tehát, hogy ha a, b, c a T töröttvonal három tetszőleges oldala, akkor az F(a), F(b), F(c) félsíkoknak van közös pontjuk.
3. Helly tételéből következik, hogy ekkor az összes F(a) félsíknak is van közös pontja, * legyen ez a közös pont Q. Állítjuk, hogy Q megfelel a feladat állításának. Először a következőt látjuk be: ha e a Q-t tartalmazó egyenes, akkor e-nek S belsejébe és határára eső pontjai egy AB szakaszt alkotnak, és ennek a szakasznak az A, B, Q pontokon kívül minden pontja belső pontja S-nek.
T nem metszi önmagát, így e és S közös része olyan A1B1, ..., AnBn szakaszokból áll, amelyekre Ai, Bi határpontja S-nek , (vagyis a T töröttvonalon van), az AiBi szakasz belseje S belsejében van és két különböző AiBi szakasznak nincs közös belső pontja (3. ábra).
 

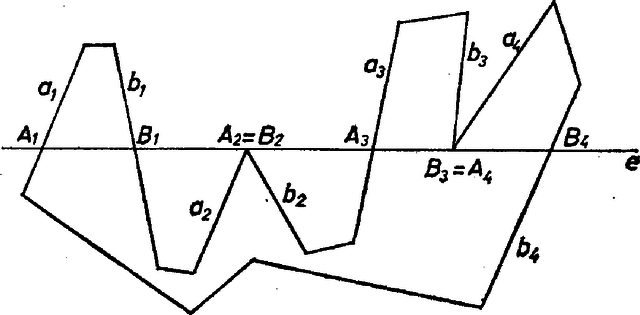3. ábra
 
Előfordulhat, hogy némelyik szakasz csak egy pont, azaz Ai=Bi (Ez az eset akkor állhat elő, ha e egy csúcsban metszi T-t, és a csúcsban találkozó két oldal e-nek ugyanazon az oldalán fekszik.) Minden AiBi szakaszhoz kiválasztható T-nek egy-egy Ai-t, ill. Bi-t tartalmazó ai, ill. bi oldala úgy, hogy az F(ai) és F(bi) közös része e-ből éppen az AiBi szakaszt tartalmazza. Másrészt Q rajta van az e egyenesen és minden F(ai) félsíkban benne van, következésképp Q rajta van az összes AiBi szakaszon. Minthogy két AiBi szakasznak nincs közös belső pontja, ebből már következik, hogy vagy m=1 és Q rajta van A1B1-en, vagy m=2 és Q=A2=B1. Az e egyenes és S közös része mindkét esetben egy AB szakasz, és A-n, B-n és Q-n kívül ennek a szakasznak minden pontja belső pontja S-nek.
4. Legyen D tetszőleges belső vagy határpontja S-nek. Belátjuk, hogy a DQ szakasz pontjai belső pontjai S-nek (D-ről és Q-ról eleve tudjuk, hogy belső- vagy határpontok). A DQ egyenest is jelöljük e-vel. e tartalmazza Q-t, így a 3.-ban bizonyítottak szerint e és S közös pontjai egy olyan A'B' szakaszt alkotnak, amelynek A'-n, B'-n és Q'-n kívül minden pontja S-nek belső pontja. D belső vagy határpontja S-nek, így rajta van az A'B' szakaszon, feltehető, hogy az A'Q szakaszon van. DQ ekkor része az A'Q szakasznak, márpedig ez utóbbinak minden belső pontja belső pontja S-nek. Ugyanez áll tehát DQ-ra is, ahogy állítottuk.
Ezzel beláttuk, hogy Q teljesíti a feladatban követelteket.
 

Megjegyzés. A feladat feltételében P-ről nem szükséges megkövetelni, hogy S-nek belső pontja legyen (lehet határpont is). A Q-ról kimondott állításnál viszont mindenképpen meg kell engedni, hogy határpont is lehessen. A 4. ábra egy olyan hatszöget mutat, amelynek bármely három belső pontjához van megfelelő P pont a hatszög belsejében, Q mégis egyértelműen meghatározott és S határán van.
 

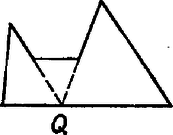4. ábra
 
*Helly tétele általában azt mondja ki, hogy ha adott a síkon véges sok konvex halmaz, melyek közül bármely háromnak van közös pontja, akkor az összesnek is van közös pontja. Lásd; Bárány Imre: Helly tételéről c. cikkét a KöMaL 1981. 2. számában 61-66. oldal.