Kezdőlap


Feladat:	Pontversenyen kívüli P.336	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1980/november, 154 - 156. oldal		PDF \| MathML
Témakör(ök):	Trigonometrikus egyenletek, Szögfüggvények, síkgeometriai számítások, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1980/május: Pontversenyen kívüli P.336

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az előírás $D F E ∢ = D E F ∢$ következményéből indulunk ki. Legyen $D$ vetülete $A C$ -re $D'$ és $D E C ∢ = ε_{2}$ . A szögfelező osztásaránya alapján a szokásos jelölésekkel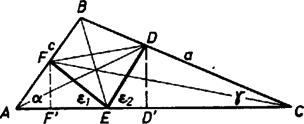

\begin{matrix} tg ε_{2} = \frac{D D'}{E D'} = \frac{C D sin γ}{C E - C D cos γ} = \frac{\frac{a b}{b + c} sin γ}{\frac{a b}{a + c} - \frac{a b}{b + c} cos γ} = \\ = \frac{a sin γ + c sin γ}{c (1 - cos γ) + (b - a cos γ)} = \frac{c (sin α + sin γ)}{c (1 - cos γ + cos α)} . \end{matrix}

Átbetűzéssel az

F E A ∢ = ε_{1}

szögre

\begin{matrix} tg ε_{1} = \frac{sin α + sin γ}{1 - cos α + cos γ}, \end{matrix}

további alakításokkal

\begin{matrix} tg D E F ∢ = - tg (ε_{1} + ε_{2}) = \frac{sin α + sin γ}{cos β + \frac{1}{2}}, \end{matrix}

és átbetűzéssel

\begin{matrix} tg D E F ∢ = \frac{sin α + sin β}{cos γ + \frac{1}{2}} . \end{matrix}

(1)

Innen is kiadódik a 2239. feladat^{$^{*}$}állítása:

γ = 120^{\circ}

esetén

F D ⊥ F E

. Nem okozhat zavart ‐ mert csak elfajult háromszögre vezethetne ‐ valamelyik nevező eltűnése, amikor e két kifejezés egyenlőségét követeljük:

\begin{matrix} \frac{sin α + sin γ}{cos β + \frac{1}{2}} = \frac{sin α + sin β}{cos γ + \frac{1}{2}} . \end{matrix}

Ha ez teljesül, akkor az

\begin{matrix} \frac{x}{y} = \frac{z}{u} \Leftrightarrow \frac{x - z}{y - u} = \frac{x}{y} \end{matrix}

(2)

azonosság alapján

\begin{matrix} tg D E F ∢ = \frac{sin γ - sin β}{cos β - cos γ} = ctg \frac{β + γ}{2} = tg \frac{α}{2} . \end{matrix}

Eszerint a vizsgált háromszögekben

\begin{matrix} D E F ∢ = D F E ∢ = \frac{α}{2} = 90^{\circ} - \frac{E D F ∢}{2}, tg E D F ∢ = - tg α, \end{matrix}

(vagyis a

D E F

háromszög köré írt kör átmegy

A

-n), és felírva

tg E D F

(1) szerinti kifejezését

\begin{matrix} \frac{sin β + sin γ}{cos α + \frac{1}{2}} = - \frac{sin α}{cos α}, (α \neq \frac{π}{2}, \frac{2 π}{3}), \end{matrix}

majd ismét (2)-t alkalmazva

\begin{matrix} sin β + sin γ + sin α = - \frac{sin α}{2 cos α} . \end{matrix}

(3)

Ennyit tüstént kiolvashatunk innen:

α > π / 2

. A bal oldalon

a < b + c

alapján

\begin{matrix} sin α < sin β + sin γ < 2 sin \frac{β + γ}{2} = 2 cos \frac{α}{2} = \frac{sin α}{sin \frac{α}{2}} \end{matrix}

(ugyanis

β = γ

eleve kizárt). Így (3)-ból

\begin{matrix} 2 sin α < sin α + sin β + sin γ = - \frac{sin α}{2 cos α} < sin α (1 + \frac{1}{sin \frac{α}{2}}), \end{matrix}

és szorozva a következő kifejezéssel

\begin{matrix} - \frac{2 cos α sin \frac{α}{2}}{sin α} = \frac{2 sin \frac{α}{2} (2 sin^{2} \frac{α}{2} - 1)}{sin α}, (> 0), \end{matrix}

valamint bevezetve a

\begin{matrix} sin \frac{α}{2} = z \end{matrix}

rövidítést:

\begin{matrix} 4 z (2 z^{2} - 1) < z < 2 (z + 1) (2 z^{2} - 1) . \end{matrix}

Az egyenlőtlenség‐lánc első feléből

z > 0

alapján

\begin{matrix} 0 < z < \sqrt[]{\frac{5}{8}} = 0, 790 569 4, \end{matrix}

(4)

a második feléből pedig

\begin{matrix} f (z) = 4 z^{3} + 4 z^{2} - 3 z - 2 > 0. \end{matrix}

f

-nek maximuma van egy negatív helyen és minimuma

(- 2 + \sqrt[]{13}) / 6

-nál (

z = 0, 27

körül), továbbá

f (0) < 0

és

f (\sqrt[]{5 / 8}) = 0, 105 > 0

. Így egyetlen pozitív zérushelye van, és az megfelel (4)-nek.

Kis kalkulátorral közelítve

f

z = 0, 780 7764

és

0, 780 776 41

helyek közt válik pozitívvá (értéke

- 7 \cdot 10^{- 8}

, ill.

+ 4 \cdot 10^{- 8}

). Eszerint

\begin{matrix} 0, 780 776 41 < sin \frac{α}{2} < 0, 790 569 4, \end{matrix}

másképpen

\begin{matrix} 102, 663 43^{\circ} & < α < 104, 4775^{\circ}, & (5) \\ 102^{\circ} 39' 48, 4'' & < α < 104^{\circ} 28' 39'' \end{matrix}

elegendő feltétel ahhoz, hogy a

D E F

háromszög egyenlő szárú legyen.

Itt választott

α

-hoz a további szögek a

β + γ = 180^{\circ} - α

és (3) rendszerből kiszámíthatók.
Megemlítjük, hogy a szűk (5) intervallumba beleesik az F. 2264-ben vizsgált

α = 4 π / 7 = 102^{\circ} 51' 25, 7''

érték. ¹
A problémát G. Parry oldotta meg a The Mathematical Gazette c. folyóirat 420. számában (1978. június).
B. T.

^{$^{*}$}K. M. L. 60 (1980) 206. oldal (1980. május).

¹Lásd a megoldást K. M. L. 61 (1980). 137. o.