Feladat: Pontversenyen kívüli P.331 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Feledi György 
Füzet: 1981/február, 74 - 75. oldal  PDF  |  MathML 
Témakör(ök): Különleges függvények, Konstruktív megoldási módszer, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1980/március: Pontversenyen kívüli P.331

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Páratlan n-re könnyen konstruálhatunk megfelelő függvényt, például úgy, hogy veszünk n darab fél‐hullámot a szinusz‐függvényből, és ezek együttesét megfelelő módon eltoljuk. A konstrukciót n=3 mellett az ábra mutatja. Ha képzeletben téglalapba zárjuk az egyes blokkokat, az egymáshoz csatlakozó téglalapok átlósan a végtelenből a végtelenbe futó lépcsőt alkotnak.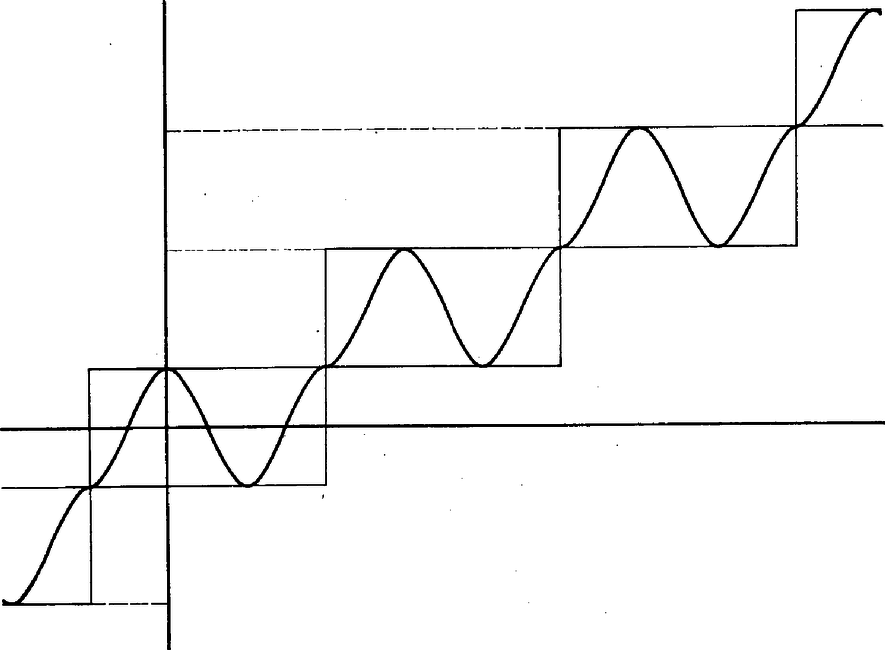


Megmutatjuk, hogy páros n-re nem létezik megfelelő függvény. Tegyük fel, hogy állításunkkal ellentétben a mindenütt értelmezett és folytonos f függvény minden valós számot pontosan n-szer vesz fel, és n páros. Vegye fel f a 0-t az
x1<x2<...<xn
helyeken, és legyen
yi=(xi+xi+1)/2,i=1,2,...,n-1,ε=12min1≤i<n|f(yi)|.

Akkor Bolzano tétele szerint xi és xi+1 között kétszer is felveszi f az ε értéket, ha f(yi)>0, ha pedig f(yi)<0, akkor a -ε értéket veszi fel kétszer ebben az intervallumban az f függvény.
Jelöljük P-vel, illetve N-nel az {f(yi), i=1,2,...,n-1} számok között a pozitívak, illetve negatívak számát, akkor f legalább 2P-szer felveszi az ε értéket és legalább 2N-szer a (-ε) értéket. Mivel N+P=n-1, és f minden értéket pontosan n-szer vesz fel, 2N és 2P közül a nagyobbik n-nel egyenlő, a kisebbik (n-2)-vel. Feltehetjük, hogy 2P=n, hiszen különben f-et (-1)-gyel szorozva juthatunk erre az esetre. Jelöljük még f-nek (x1,xn) feletti maximumát M-mel. Mivel f folytonos, M véges. Ámde ekkor f sehol sem veheti fel az M+1 értéket. Nem veheti fel ugyanis f az (M+1)-et x1 előtt vagy xn után, hiszen akkor újabb helyen venné fel az ε értéket is. M definíciója folytán x1 és xn között sem veheti fel f az (M+1) értéket, így ellentmondásra jutottunk, és eredeti állításunkat ezzel bebizonyítottuk.
 

 Feledi György (Bp., Fazekas M. Gyak. Gimn., III. o. t.)