Feladat: Pontversenyen kívüli P.302 Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 1981/február, 73 - 74. oldal  PDF  |  MathML 
Témakör(ök): Számsorozatok, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1978/április: Pontversenyen kívüli P.302

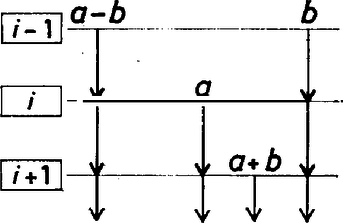
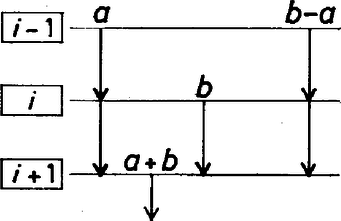
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Nevezzük az a és b számokat (ebben a sorrendben) szomszédosnak, ha az eljárás folyamán előáll egy olyan szakasz, melynek bal oldali végpontjában a, a jobb oldaliban pedig b áll. Így például az 1. ábra alapján 1 és 2, 3 és 2, 3 és 5 mind szomszédosak. Elsőként belátjuk, hogy a szomszédos számok relatív prímek. Ezt az összegükre vonatkozó teljes indukcióval tesszük.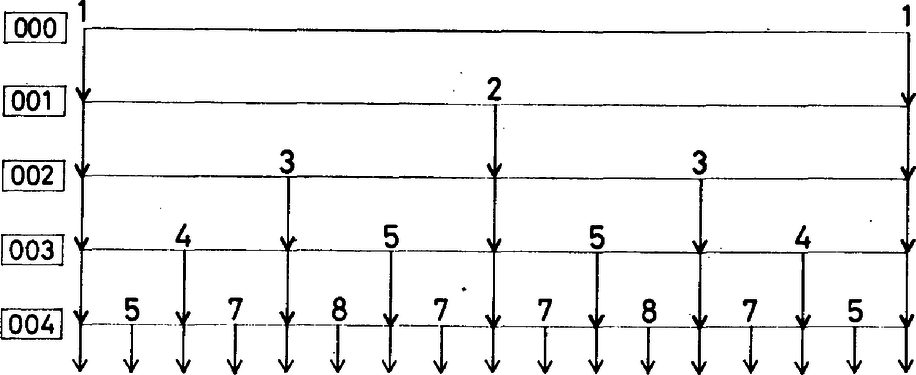
Az eljárás folyamán pozitív egész számok összegét írjuk a szakasz egy‐egy pontja fölé (1. ábra). Így ha a és b szomszédosak és a+b≤2, akkor csak a=b=1 lehetséges, és ezek valóban relatív prímek.

 

1. ábra
 

Tegyük fel most, hogy a és b szomszédosak, és az i-edik lépésben álltak elő. Ez csak kétféleképpen lehetséges: vagy a>b és az (i-1)-edik lépésben a-b és b szomszédosak voltak (2/a ábra), vagy pedig a<b és az (i-1)-edik lépésben a és b-a volt szomszédos (2/b ábra). Mivel (a-b)+b<a+b, és a-b és b szomszédosak [illetve a+(b-a)<a+b és a és b-a szomszédosak], azért az indukciós feltevésünk szerint a-b és b (illetve a és b-a) relatív prímek, amiből azonnal adódik, hogy a és b is relatív prímek.
Meggondolásunkból az is adódik, hogy minden (a,b) számpár legfeljebb egyszer fordulhat elő szomszédosakként. Valóban, az (1, 1) számpár egyszer szerepel, és ha az (a,b) számpár kétszer szerepelne, akkor az (a-b,b) pár illetve az (a,b-a) pár is kétszer szerepelne.
 
2a. ábra
 
2b. ábra

Végül megmutatjuk, hogy ha a és b relatív prímek, akkor a és b szomszédosak (és az előbbi megjegyzésünk szerint ekkor pontosan egyszer szerepelnek). Ezt ismét (a+b)-re vonatkozó indukcióval látjuk be. Az a+b≤2 esetben ha a és b relatív prímek, akkor a=b=1, ezek pedig szomszédosak.
Ha a+b>2, akkor a és b különböző, például a>b. Ekkor a-b és b is relatív prímek, és összegükre (a-b)+b<a+b. Indukciós feltevésünk szerint a-b és b szomszédosak, s az eljárás során az általuk meghatározott szakasz felezőpontjához az összegük, a kerül, tehát a és b is szomszédosak. Hasonlóan intézhető el az a<b eset.
Az 1978 szám annyiszor szerepel, ahányféleképpen elő lehet állítani egymáshoz relatív prím számok összegeként (természetesen a+b és b+a különböző előállításnak számít). Ez pedig megegyezik az 1978-nál kisebb, hozzá relatív prímek számával, vagyis 924-gyel. Az egymilliomodik felezés után csak milliónál nagyobb számok kerülhetnek a szakasz végpontjaihoz, így mind a 924 számpár szerepel az eddig felírtak között.
Tehát a felírt számok között az 1978 szám 924-szer fog szerepelni.