Kezdőlap


Feladat:	Pontversenyen kívüli P.282	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Erdélyi T. , Horváth 219 J. , Ruisz T. , Seress Ákos , Vándor T.
Füzet:	1978/október, 70 - 71. oldal		PDF \| MathML
Témakör(ök):	Forgatva nyújtás, Körülírt kör, Beírt kör, Magasságpont, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1977/március: Pontversenyen kívüli P.282

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $A B C$ háromszög körülírt körének középpontját $K$ -val, beírt körének érintési pontjait az oldalakon $A_{1}, B_{1}, C_{1}$ -gyel, középpontját $O$ -val. Az $A O, B O, C O$ messe az $A B C$ háromszög körülírt körét rendre az $A_{2}, B_{2}, C_{2}$ pontokban. ( $A_{2}$ felezi a $B C$ ívet, hasonló mondható $B_{2}$ és $C_{2}$ -ről is.) Az $A_{1} B_{1} C_{1}$ háromszög magasságpontja $M$ ; belátjuk, hogy $K, O$ és $M$ egy egyenesen vannak.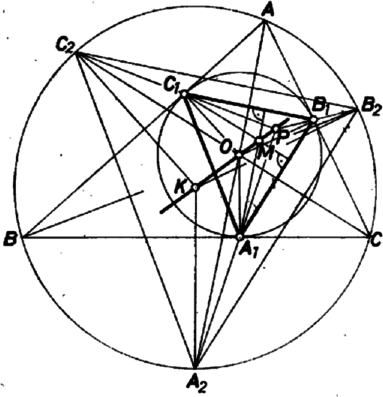

Legyen

P

a beírt és körülírt körnek az a hasonlósági pontja, amelyből pozitív arányú nyújtással vihetők egymásba. Nyilvánvalóan

P

O K

egyenesen van. (Az

O = K

esetben az állítás triviális, tehát ezt nem vizsgáljuk.)

P

-ből nagyítsuk fel a beírt kört úgy, hogy

O

K

pontba menjen át.

P

hasonlósági középpont, így a beírt kör képe a körülírt kör.

O A_{1}

képe a körülírt kör

O A_{1}

-gyel párhuzamos, vele egyirányú sugara, tehát

K A_{2}

. Hasonlóan

C_{1}

képe

C_{2}, B_{1}

képe

B_{2}

. Belátjuk még, hogy

M

képe

O

; ezzel a bizonyítás kész, hiszen ekkor

P, O

és

M

egy egyenesen vannak; másfelől

P, O

és

K

is egy egyenesen vannak, így

M

rajta van az

O K

egyenesen.
Láttuk, hogy

A_{1} B_{1} C_{1}

háromszög képe az

A_{2} B_{2} C_{2}

háromszög. Így elég belátnunk, hogy az

A_{2} B_{2} C_{2}

háromszög magasságpontja

O

. Az

A C_{1} O B_{1}

négyszög deltoid, mert

A C_{1} = A B_{1}

(ezek ui. külső pontból egy körhöz húzott érintők) és

C_{1} O = O B_{1}

(mindkettő a beírt kör sugara). Így

A O

merőleges

C_{1} B_{1}

-re, a nagyítás miatt

C_{1} B_{1}

párhuzamos

C_{2} B_{2}

-vel, így

A A_{2}

merőleges

C_{2} B_{2}

-re. Hasonlóan belátható, hogy

B B_{2}

és

C C_{2}

is az

A_{2} B_{2} C_{2}

háromszög magasságvonalai.
Ezzel a bizonyítást befejeztük.

Seress Ákos (Budapest, Fazekas M. Gyak. Gimn.)