Kezdőlap


Feladat:	Pontversenyen kívüli P.274	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Csikós Balázs , Erdélyi Tamás , Knébel István , Seress Ákos
Füzet:	1979/május, 212 - 213. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Háromszögek nevezetes tételei, Szinusztétel alkalmazása, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1976/november: Pontversenyen kívüli P.274

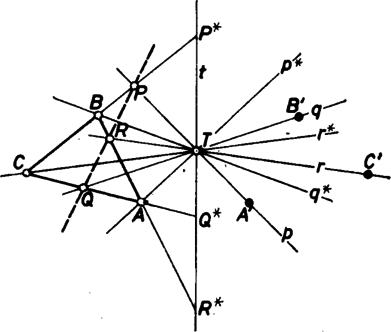
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Nyilván fel kell tennünk, hogy $T$ különbözik az $A$ , $B$ , $C$ pontoktól, különben $p$ , $q$ , $r$ nincs meghatározva. Párhuzamos egyenesek metszéspontját szokásos módon ideális, végtelen távoli pontként értelmezve, kiterjeszthető a feladat állítása, ezt az általános alakot bizonyítjuk.

Jelöljük

t

-nek a

B C

C A

A B

egyenesekkel alkotott metszéspontját rendre

P^{*}

-gal,

Q^{*}

-gal,

R^{*}

-gal. Irányítsuk tetszőlegesen a

p

q

r

és

t

egyeneseket, és jelöljük

p

-nek,

q

-nak,

r

-nek

t

-re vonatkozó tükörképét

p^{*}

-gal,

q^{*}

-gal,

r^{*}

-gal. Menelaosz tétele szerint abból, hogy

P^{*}

Q^{*}

R^{*}

egy egyenesen vannak, következik, hogy

\begin{matrix} (A B R^{*}) (B C P^{*}) (C A Q^{*}) = - 1, \end{matrix}

és ha belátjuk, hogy

\begin{matrix} (A B R) (B C P) (C A Q) = - 1, \end{matrix}

ebből következik, hogy

P

Q

R

is egy egyenesen vannak. Elég tehát belátni, hogy

\begin{matrix} (A B R R^{*}) (B C P P^{*}) (C A Q Q^{*}) = 1, \end{matrix}

(1)

ahol például

(A B R R^{*}) = (A B R) : (A B R^{*})

, és

(A B R) = A R : R B

. (A felhasznált tételek és fogalmak megtalálhatók Hajós Gy.: Bevezetés geometriába c. könyvében.) Papposz tétele szerint (1) helyett elegendő belátnunk, hogy

\begin{matrix} (p^{*} q^{*} r t) (q^{*} r^{*} p t) (r^{*} p^{*} q t) = 1. \end{matrix}

(2)

Jelöljük a

t

irányított egyenest

p

q

r

-be vivő forgatások nagyságát rendre

α

β

γ

-val, akkor a kettős viszony definíciója szerint

\begin{matrix} (p^{*} q^{*} r t) = & \frac{sin (α + γ)}{sin (β + γ)} : \frac{sin α}{sin β}, \\ (q^{*} r^{*} p t) = & \frac{sin (β + α)}{sin (γ + α)} : \frac{sin β}{sin γ}, \\ (r^{*} p^{*} q t) = & \frac{sin (γ + β)}{sin (α + β)} : \frac{sin γ}{sin α} . \end{matrix}

Ebből pedig közvetlenül következik a bizonyítandó (2) összefüggés.