Kezdőlap


Feladat:	Pontversenyen kívüli P.270	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Tar József
Füzet:	1978/november, 153 - 155. oldal		PDF \| MathML
Témakör(ök):	Függvényvizsgálat differenciálszámítással, Sorozat határértéke, Rekurzív eljárások, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1976/május: Pontversenyen kívüli P.270

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $a^{x}$ függvényt $f (x)$ -szel. Sorozatunk ebből az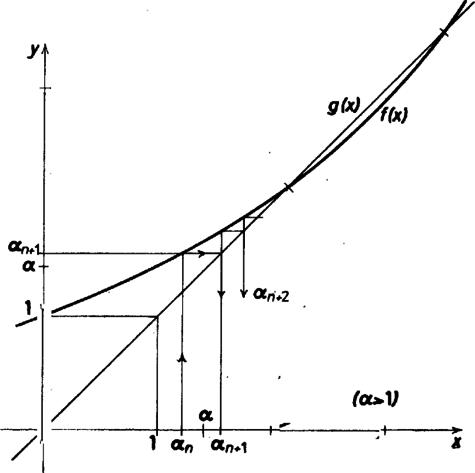

\begin{matrix} α_{n + 1} = f (α_{n}) \end{matrix}

helyettesítéssel kapható. Annak érdekében, hogy egy adott

α_{n}

-ból kiindulva a sorozat további tagjait geometriailag szemléltethessük, rajzoljuk fel a

g (x) = x

függvényt is az

f (x)

képe mellé. Ennek segítségével az

α_{n + 1}

ordinátát átfordíthatjuk abszcisszává, és kikereshetjük

f

itt felvett értékét. Tehát az

x

tengely

α

abszcisszájú pontjából indulva ,,felmegyünk'' az (

α

f (α)

) pontba, innen az

x

tengellyel párhuzamosan átmegyünk az (

α_{1}

α_{1}

) pontba, majd megint az

y

tengellyel párhuzamosan haladva az (

α_{1}

f (α_{1})

) ponton át folytatjuk utunkat.

α = 1

α_{n}

értéke is

1

, a sorozat tagjai egyenlőek. Ha

α > 1

f (x)

monoton nő, tehát a sorozat is nő. Sorsát az határozza meg, hogy metszi-e

f (x)

g (x)

-et vagy sem. Ha metszi, a sorozat ,,beleütközik'' ebbe a gyökbe, nem léphet rajta túl, és ezt fokozatosan megközelíti. Mivel

f (0) = 1 > g (0)

, az

\begin{matrix} f (x) = g (x) \end{matrix}

(1)

egyenlet legkisebb pozitív gyökét

β

-val jelölve látható, hogy

0 < x < β

mellett

x < f (x) < β

. Ha tehát az

α_{- 1} = 1

értékből indulunk ki, az

α_{0} = f (1) = α, ..., α_{n + 1} = f (α_{n})

sorozat tagjai monoton nőnek, és mindegyik kisebb

β

-nál. Emiatt a sorozat konvergál, és határértéke gyöke

(1)

-nek.
Ha különböző

α

-k mellett vizsgáljuk egy adott pozitív

x

-ben az

f (x)

függvényértékeket, a monoton növekvő

φ (α) = α^{x}

függvényt kapjuk. Emiatt

(1)

gyöke

α

monoton növekvő függvénye. Ahogy növeljük

α

-t, úgy emelkedik az

f (x)

függvény görbéje, és egy bizonyos

α_{max}

-ot túllépve olyan

α

-kat kapunk, amelyek mellett

(1)

-nek egyáltalán nincs gyöke. Ilyen például az

α = e

érték, hiszen emellett

f' (x) = e^{x} > g' (x) = 1

; ha

x > 0

, az

f - g

különbség monoton nő. Ha

α = α_{max}

mellett az

f

és

g

függvénygörbék érintik egymást, emiatt

α_{max}

\begin{matrix} f' (x) = g' (x) \end{matrix}

(2)

egyenletnek is gyöke. (Ezt itt a szemlélet alapján fogadjuk el, de nem nehéz belátni az állításunk helyességét.) Az

(1) - (2)

egyenletrendszerből kapjuk, hogy

\begin{matrix} α_{max} = e^{1 / e} \end{matrix}

α_{n}

sorozat

α > α_{max}

esetén is monoton nő, de nem lehet korlátos, hiszen akkor konvergens volna, és

(1)

-nek lenne gyöke. Így ebben az esetben csak az lehet, hogy

\begin{matrix} {lim}_{n \to \infty}^{} α_{n} = \infty . \end{matrix}

0 < α < 1

, az

f (x)

függvény monoton fogy, és

(1)

-nek egyetlen gyöke van a

0 < x < 1

intervallumban. Most

0 < α_{1} < α_{0} < 1

, tehát

\begin{matrix} f (0) = 1 > f (α_{1}) = α_{2} > f (α_{0}) = α_{1} > f (1) = α_{0} . \end{matrix}

Hasonlóan tovább haladva kapjuk, hogy

0 < α_{n} < 1

, és az

α_{2 k}

sorozat monoton nő,

α_{2 k + 1}

pedig monoton fogy. Így az

α_{n}

sorozat most is konvergens, és határértéke

(1)

egyetlen gyöke. Azt kapjuk tehát, hogy ha

0 < α \leq e^{1 / e} (= 1, 4446678)

, az

α_{n}

sorozat konvergens, és határértéke

(1)

kisebbik pozitív gyöke. Különben

α_{n}

végtelenbe tart.

Tar József (Eger, Gárdonyi G. Gimn.)