Feladat: Pontversenyen kívüli P.270 Korcsoport: 18- Nehézségi fok: -
Megoldó(k):  Tar József 
Füzet: 1979/december, 215 - 216. oldal  PDF  |  MathML 
Témakör(ök): Függvényvizsgálat differenciálszámítással, Sorozat határértéke, Rekurzív eljárások, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1976/május: Pontversenyen kívüli P.270

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A korábban közölt megoldásnak (KÖMAL 1978/8‐9., 153‐155. oldal) az α≥1 esettel foglalkozó része lényegében helyes. A 0<α<1 esetben az még igaz, hogy α2k monoton nő és α2k+1 monoton fogy (bár ennek bizonyításába is hiba ‐ talán sajtóhiba ‐ csúszott, hiszen most α0 nem nagyobb α1-nél, hanem csakúgy, mint az α2k részsorozat minden tagja, kisebb α1-nél is, és az α2k+1 részsorozat minden más tagjánál is). Ebből azonban ‐ még ha azt is felhasználjuk, hogy a sorozat korlátos ‐ csak annyi következik, hogy az α2k részsorozat is konvergens és az α2k+1 részsorozat is konvergens, az azonban nem biztos, hogy a két sorozat határértéke megegyezik. Most ugyanis csak annyit tudunk a két részsorozat határértékéről a képzési szabály alapján, hogy ha őket rendre β-val, γ-val jelöljük, akkor gyökei a

β=f(γ),γ=f(β)(1)
egyenletrendszernek, ahol f(x) most is az αx függvényt jelöli. Amennyiben (1)-nek több gyökpárja van, azokra egyrészt nyilván 0<β, γ<1 teljesül, másrészt a β, γ határértékekről még azt is tudjuk, hogy β≤γ épp az előbb említett α2k<α2k+1 összefüggés miatt. A megoldás első felében alkalmazott meggondoláshoz hasonlóan az is belátható, hogy az (1) gyökpárjai közül a (β,γ) az, amelyben β a legkisebb, és ennek megfelelően γ a legnagyobb.
Azt kell tehát megvizsgálnunk, van-e (1)-nek olyan gyökpárja, amelyben β<γ. Jelöljük f inverzét φ-vel: φ(x)=logαx. Mivel (1) első egyenlete alapján γ=φ(β) az
f(x)-φ(x)=0(2)
egyenlet legkisebb gyöke, ennek az egyenletnek biztosan gyöke az
f(x)=x,(3a)φ(x)=x(3b)


egyenletek egyetlen közös x0 gyöke, a kérdés csak az, hogy itt az f,φ függvények képei milyen irányban metszik át egymást.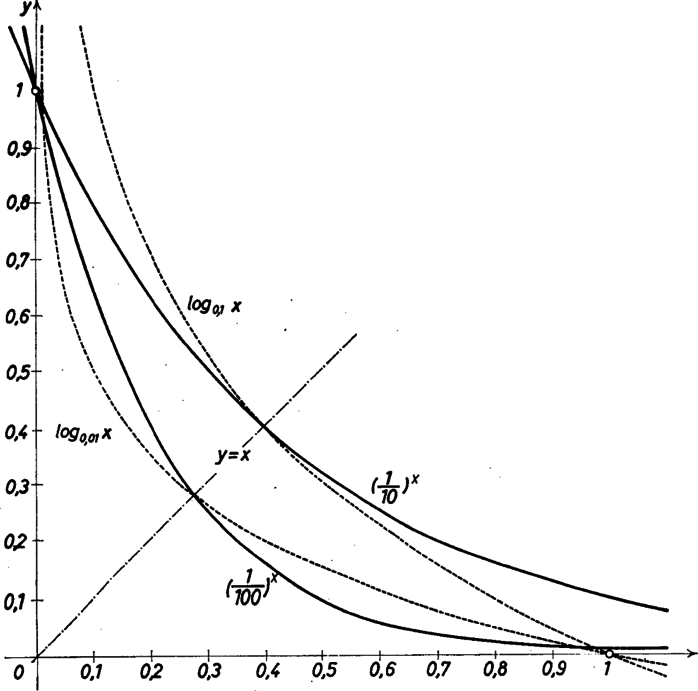
 
 

Ha ugyanis f'(x0)-φ'(x0)<0, akkor
limx→0[f(x)-φ(x)]=-∞

miatt (2)-nek biztosan létezik x0-nál kisebb gyöke. Másrészt mivel f'(x)=f(x)⋅logeα és φ'(x0)=1/f'(x0), azért f'(x0)-φ'(x0)≥0 pontosan akkor teljesül, ha x0logeα≥-1, vagyis
ex0logeα=αx0=x0≥e-1,logeα≥-1x0≥-e,ahonnanα≥1/ee.

Ebben az esetben az f(x)-φ(x) függvény x>0-ra szigorúan monoton nő, hiszen deriváltjának x-szerese
x(f'(x)-φ'(x))=x⋅f(x)⋅logeα-1logeα≥-1e-1logeα≥0,
tehát (2)-nek legfeljebb egy gyöke lehet.
Összefoglalva, a vizsgált sorozat csak akkor konvergens, ha
1/ee≤α≤e1/e,
ha viszont 0<α<1/ee, akkor az α2k,α2k+1 részsorozatok ugyan konvergensek, de határértékük különböző.
 Magyar Zoltán levele alapján