Kezdőlap


Feladat:	Pontversenyen kívüli P.244	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Déri Attila , Lang Gyula , Lévai László , Seress Ákos
Füzet:	1978/november, 149 - 151. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Kocka, Hossz, kerület, Hatványközepek közötti egyenlőtlenség, Szélsőérték-feladatok differenciálszámítás nélkül, Térgeometriai számítások trigonometria nélkül, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1975/március: Pontversenyen kívüli P.244

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük az egységnyi élű $A B C D E F G H$ kocka $A E$ , $B C$ és $G H$ kitérő éleinek egy-egy pontját rendre $L$ , $M$ , $N$ -nel. Legyen $A L = x$ , $C M = y$ és $H N = z$ . Célunk, hogy meghatározzuk, $x$ , $y$ , $z$ mely értékeire lesz az $L M N$ háromszög kerülete minimális.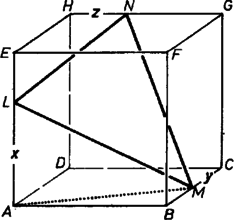

Az oldalak hosszát Pitagorasz tétele segítségével fejezzük ki. Az

A B M

háromszögből

A M = \sqrt[]{1 + {(1 - y)}^{2}}

, az

L A M

háromszögből

L M = \sqrt[]{x^{2} + {(1 - y)}^{2} + 1}

. Hasonlóan

M N = \sqrt[]{1 + y^{2} + {(1 - z)}^{2}}

és

N L = \sqrt[]{{(1 - x)}^{2} + 1 + z^{2}}

. Jelöljük ezek összegét

K

-val. Némi átalakítás után

K

-t alulról becsülhetjük a számtani és a négyzetes közép közötti összefüggés segítségével.

\begin{matrix} K = \sqrt[]{6} (\sqrt[]{\frac{x^{2} + {(1 - y)}^{2} + 4 {(\frac{1}{2})}^{2}}{6}} + \sqrt[]{\frac{4 {(\frac{1}{2})}^{2} + y^{2} + {(1 - z)}^{2}}{6}} + \\ + \sqrt[]{\frac{{(1 - x)}^{2} + 4 {(\frac{1}{2})}^{2} + z^{2}}{6}}) \geq \\ \geq \sqrt[]{6} (\frac{x + (1 - y) + 4 (\frac{1}{2})}{6} + \frac{4 (\frac{1}{2}) + y + (1 - z)}{6} + \frac{(1 - x) + 4 (\frac{1}{2}) + z}{6}) = \frac{3}{2} \sqrt[]{6} . \end{matrix}

Tehát

K \geq \frac{3}{2} \sqrt[]{6}

, és egyenlőség csak az

x = y = z = \frac{1}{2} = 1 - x = 1 - y = 1 - z

esetben áll fenn, azaz ha az

L M N

háromszög csúcsai a megfelelő élek felezőpontjai.

Seress Ákos (Budapest, Fazekas M. Gyak. Gimn.)

II. megoldás. Jelöljük a kitérő éleket

p

q

r

-rel, felezőpontjaikat

P

Q

R

-rel. Megmutatjuk, hogy a

P Q R

háromszög kerülete minimális a vizsgált háromszögek között. Jelöljük a

P Q R

háromszög síkját

S

-sel, és tükrözzük a kockát az

r

-en átmenő,

S

-re merőleges síkra. Mivel a kocka centruma benne van

S

-ben, az a sík, amire tükrözünk

p

-vel,

q

-val

45^{\circ}

-os szöget zár be. Emiatt

p

tükörképe benne marad a

p

-n átmenő,

r

-re merőleges lap síkjában, és merőleges

p

-re. Jelöljük ezt

p_{1}

-gyel,

q

P

Q

tükörképét

q_{1}

P_{1}

Q_{1}

-gyel. Mivel

S

merőleges a tükrözés síkjára,

P_{1}

Q_{1}

is benne lesz

S

-ben.
Hasonlóan tovább menve lépésről lépésre tükrözzünk a

q_{1}

-en,

p_{2}

-n,

r_{3}

-on,

q_{4}

-en átmenő,

S

-re merőleges síkokra, az

(i + 1)

-edik tükrözés után

p_{i}

q_{i}

r_{i}

tükörképét

p_{i + 1}

q_{i + 1}

r_{i + 1}

-gyel jelölve (

i = 1

2

3

4

r_{1}

azonos

r

-rel). Közben a

P

R

Q_{1}

P_{2}

R_{3}

Q_{4}

P_{5}

pontok mind egy egyenesre kerülnek. Hajtsuk végre ezeket a tükrözéseket a

p

q

r

egyenesek tetszőleges

P^{*}

Q^{*}

R^{*}

pontján is. A

P^{*} Q^{*} R^{*}

háromszög kerületének kétszerese szétnyílik a

P^{*} R^{*} Q_{1}^{*} P_{2}^{*} R_{3}^{*} Q_{4}^{*} P_{5}^{*}

töröttvonal hosszára. Ennek hossza nem lehet kisebb a

P^{*} P_{5}^{*}

szakasz hosszánál, ez viszont egyenlő

P P_{5}

hosszával és

P Q R

kerületének kétszeresével.

Megjegyzés. Ábránkon a szereplő

6

kockát egy

4 \times 3

-as alaprajzú hatszintes építménybe foglaltuk bele. Hogy a térbeli viszonyokat jobban érzékeltessük, egész közel mentünk hozzá, ezért erős perspektívikus torzulások keletkeztek.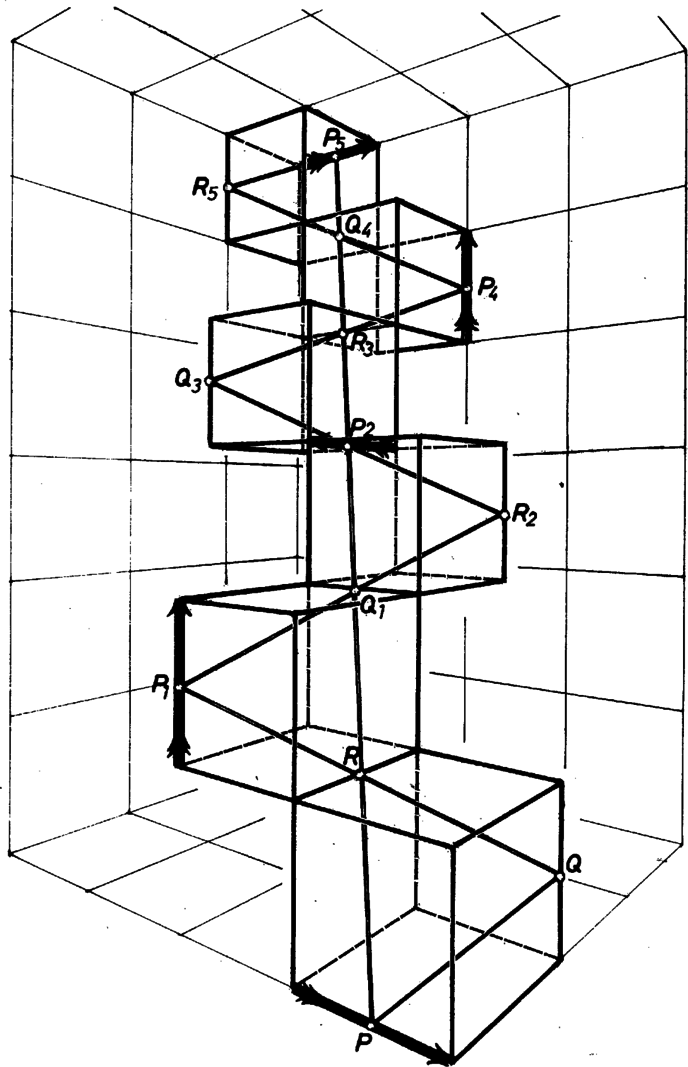