Feladat: Pontversenyen kívüli P.229 Korcsoport: 18- Nehézségi fok: -
Megoldó(k):  Surján Péter ,  Wolf György 
Füzet: 1979/január, 22 - 23. oldal  PDF  |  MathML 
Témakör(ök): Függvényvizsgálat differenciálszámítással, Sorozat határértéke, Rekurzív eljárások, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1974/december: Pontversenyen kívüli P.229

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a bn=logan sorozatot. Az an sorozatra adott összefüggésből következik, hogy

bn+1=(1+bn)⋅2-bn,b1=loga1,
továbbá liman akkor és csak akkor létezik, ha vagy limbn létezik, vagy limbn=-∞ (és ekkor liman=0). Ezért a továbbiakban csak a bn sorozattal foglalkozunk.
Tekintsük az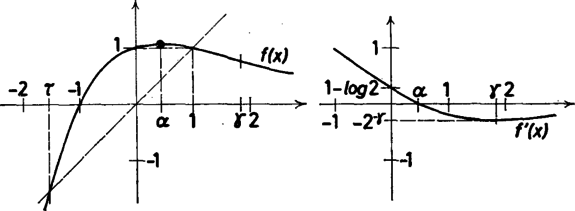
f(x)=(1+x)⋅2-x
függvényt. Ennek segítségével a rekurziót bn+1=f(bn) alakban írhatjuk. Mivel f határértéke +∞-ben 0, -∞-ben -∞, továbbá deriváltja (itt és a továbbiakban a logaritmusok e alapúak)
f'(x)=(1-log2-x⋅log2)⋅2-x
az egyetlen α=-1+1/log2≈0,443 helyen tűnik el, f ábrája olyan, mint ahogyan azt az 1. ábra mutatja. A 2. ábrán f'(x)-et ábrázoltuk, a minimumhelyet (f inflexiós pontját) az
f''(x)=log2⋅(-2+log2+x⋅log2)⋅2-x
függvény (egyetlen) zérushelye szolgáltatja: γ=-1+2/log2≈1,885. Az f' tehát a (-∞,γ] félegyenesen szigorúan monoton csökken, a [γ,+∞) félegyenesen szigorúan monoton nő, de mindig az x tengely alatt marad. Ezért x>0-ra f'(x) értéke f'(0)=1-log2≈0,307 és f'(γ)=-2-γ≈-0,271 között van, így tetszőleges pozitív ξ számra |f'(ξ)|<0,5.
 
 

Ha most bi pozitív, akkor bi+1=f(bi) is az, továbbá f(1)=1, és a Lagrange-féle középértéktételt (lásd pl. Molnár Emil: Matematikai Versenyfeladatok gyűjteménye, 521. oldal) alkalmazva
|bi+1-1|=|f(bi)-f(1)|=f'(ξ)|⋅|bi-1|≦0,5⋅|bi-1|,
(ξ az 1 és bi közé esik, tehát pozitív), vagy általában
|bi+j-1|≦|0,5j⋅|bi-1|.


Ha j→∞, akkor a jobb oldal tart a nullához, de ekkor a bal oldal is tart a nullához, vagyis limj→∞bi+j=1. Összefoglalva: ha a bn sorozatnak van pozitív tagja, a sorozat konvergens és tart 1-hez.
Abból, hogy f(-1)=0 és f(-2)=-3, következik, hogy van olyan -2<τ<-1 érték, melyre f(τ)=τ(τ≈-1,530). Az f(x)=x egyenletnek 1-en és τ-n kívül nincs más gyöke. Ugyanis ellenkező esetben a Lagrange-féle középértéktételt az f függvényre a gyökhelyeken alkalmazva azt kapnánk, hogy f'(x) az 1 értéket legalább két helyen felvenné, ellentétben korábbi megállapításainkkal. Így tehát ha x<τ, akkor f(x)<x, és ha τ<x<1, akkor f(x)>x.
Visszatérve a feladatra, b1 értékétől függően különböztessünk meg három esetet:
I. b1=τ. Ekkor mindegyik bn=τ, tehát a bn sorozat konvergens.
II. b1<τ. Most bn+1=f(bn)<bn<τ. azaz a bn sorozat monoton csökken. Így vagy van határértéke, vagy limn→∞bn=-∞.
III. b1>τ. Ha van a sorozatnak pozitív tagja, akkor egy korábbi megállapításunk szerint limbn létezik (és egyenlő 1-gyel). Ha nincs, akkor τ<bn<f(bn)=bn+1≦0 miatt a sorozat monoton növő és felülről korlátos, tehát a határérték ebben az esetben is létezik.
Összefoglalva tehát: tetszőleges bn-ből kiindulva vagy létezik limbn, vagy limbn=-∞, vagyis a liman határérték mindig létezik.