Kezdőlap


Feladat:	Pontversenyen kívüli P.227	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1976/december, 211 - 213. oldal		PDF \| MathML
Témakör(ök):	Konstruktív megoldási módszer, Egyéb sokszögek geometriája, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1974/november: Pontversenyen kívüli P.227

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a keresett sokszög csúcsait $A_{0}$ , $A_{1}$ , $...$ , $A_{n_{1}}$ -gyel, és legyen $A_{n} = A_{0}$ , $A_{n + 1} = A_{1}$ . A mondott feltételek ekvivalensek azzal, hogy

\begin{matrix} A_{i} A_{i + 1} = 1, A_{i} A_{i + 2} = \sqrt[]{2}, (i = 0, 1, ..., n - 1) . \end{matrix}

(1)

n \leq 3

, (1) ellentmondásokat tartalmaz, így csak

n \geq 4

jöhet szóba. Ha

n = 4

, a négyzet megfelel. Megmutatjuk, hogy

n = 5

mellett (1) nem megoldható. Ha ugyanis megoldható volna, az

A_{0} A_{1} A_{3}

háromszögben

A_{0} A_{1} = 1

A_{1} A_{3} = A_{0} A_{3} = \sqrt[]{2}

volna,

A_{2}

A_{4}

pedig egyrészt az

A_{0} A_{1}

szakasz síkjára merőleges,

A_{1}

, illetve

A_{0}

körüli egységsugarú

k_{2}

k_{4}

körön volna, másrészt e pontok az

A_{3}

körüli egységsugarú gömbön is rajta volnának.

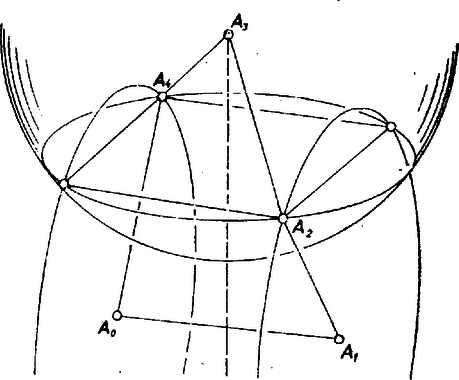1. ábra

A gömb és

k_{2}

k_{4}

metszéspontjai egy téglalapot határoznak meg, amelynek

A_{0} A_{1}

-gyel párhuzamos oldala egységnyi, tehát nem játszhatja az

A_{2} A_{4}

szakasz szerepét, és mint az némi számolással látható, átlója sem

\sqrt[]{2}

hosszú, tehát az sem lehet

A_{2} A_{4}

.
Ha

n = 6

, a keresett pontrendszer lehet például egy kocka két szomszédos lapjának hat csúcsa. Ha

n = 7

, a konstrukció a következő: induljunk ki az

A_{1} A_{2} A_{4} A_{5}

négyszögből, ebben válasszuk

A_{2} A_{4}

-t

A_{1} A_{5}

-tel párhuzamosnak,

A_{1} A_{5}

hosszát egységnyinek, és természetesen legyen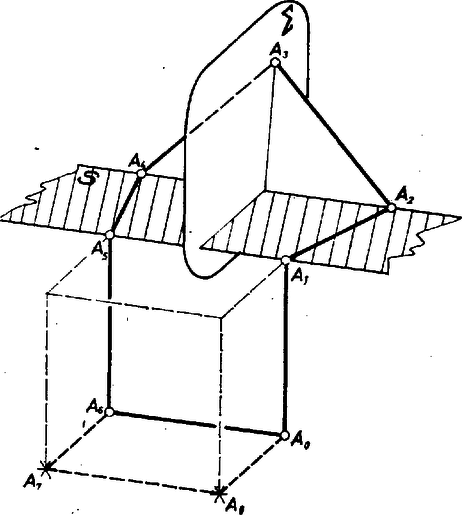

\begin{matrix} A_{1} A_{2} = 1, A_{2} A_{4} = \sqrt[]{2}, A_{4} A_{5} = 1. \end{matrix}

Jelöljük az

A_{1} A_{2} A_{4} A_{5}

trapéz síkját

S

-sel, az

S

-re merőleges, a trapéz szimmetriatengelyén átmenő síkot

\sum

-val.

2. ábra

Mivel

A_{4} A_{5}

nem merőleges

\sum

-ra, az

A_{5}

-ön átmenő,

A_{4} A_{5}

-re merőleges, és az ugyancsak

A_{5}

-ön átmenő

\sum

-val párhuzamos síkok metszik egymást. Metszésvonalukra mérjük fel az

A_{5} A_{6} = 1

szakaszt, mivel

A_{1} A_{5} ⊥ \sum

, az

A_{1} A_{5} A_{6}

háromszög egy négyzet fele, legyen

A_{0}

a négyzet hiányzó csúcsa. A hiányzó

A_{3}

pontot az

A_{2} A_{3} = 1

A_{1} A_{3} = \sqrt[]{2}

feltételek

\sum

-ban már lényegében meghatározzák. Ha itt az

A_{0} A_{1} A_{5} A_{6}

négyzetre egy kockát illesztünk, annak

A_{0} A_{6}

-hoz csatlakozó lapján megkerülhetjük az

A_{0} A_{6}

szakaszt, tehát az oldalak száma 2-vel könnyen növelhető. Hasonlóan lépkedve tovább tetszőleges páratlan

n

-re megoldást kapunk, a párosokat pedig a már tárgyalt

n = 6

esetből állíthatjuk elő.
Térben tehát az

n \leq 3

n = 5

esetek kivételével minden

n

-hez található a kívánt tulajdonságú

n

-szög.

Megjegyzés. Síkban is vizsgálható a kérdés, és belátható, hogy csak 4-gyel osztható

n

-ek jöhetnek szóba, és ezek mindegyike realizálható is, kivéve az

n = 8

esetet, ebben csak akkor kapunk megoldást, ha megengedjük, hogy például

A_{0}

és

A_{4}

azonos legyen.