Feladat: Pontversenyen kívüli P.221 Korcsoport: 18- Nehézségi fok: -
Megoldó(k):  Hasenfratz Anna ,  Seress Ákos ,  Surján Péter 
Füzet: 1975/november, 154 - 155. oldal  PDF  |  MathML 
Témakör(ök): Egyenlőtlenségek, Részhalmazok, Számhalmazok, Számelmélet alaptétele, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1974/október: Pontversenyen kívüli P.221

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen N tetszőleges szám, amely mellett a kívánt osztályozás elvégezhető, és jelöljük a kapott osztályokat A-val, B-vel. Legyen a1, a2 az A két különböző eleme, és b a B tetszőleges eleme, amelyre

b≠a1+a2,b≠a2-a1(1)
teljesül. Ha a b1=a1+a2 számot még osztályoztuk, az csak B-hez tartozhat, hiszen két különböző A-beli szám összege. Ha az a3=b1+b=a1+a2+b számot még osztályoztuk, az csak A-hoz tartozhat, hiszen két különböző B-beli összege. Ekkor a b2=a1+b szám nem tartozhat A-hoz, különben az A-beli a3 két különböző A-beli szám összege volna. Ezek szerint a c=a1+a3=b1+b2=2a1+a2+b számot már semmi esetre sem osztályozhatjuk, hiszen ez két különböző A-beli számnak is és két különböző B-beli számnak is az összege.
 

 

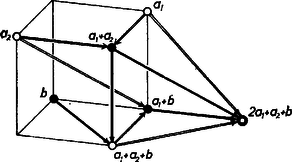Ezzel beláttuk, hogy
N<2a1+a2+b,(2)
hiszen különben az a2, a3, b1, b2, c számok mindegyikét osztályoznunk kellene, és mint megmutattuk, ez lehetetlen.
Ha az {n,n+1,...,N} számok valamely kívánt tulajdonságú osztályozásánál az n, n+1, n+2 számok nem kerülnek ugyanabba az osztályba, válasszuk A-nak azt az osztályt, amelyikbe közülük kettő került, a1-nek ezek közül a kisebbiket, a2-nek a másikat, és b legyen a harmadik. Ha n>1, ezekre teljesül (1), emiatt ilyen osztályozás csak akkor lehetséges, ha N-re teljesül a (2)-nek megfelelő
N<2a1+a2+b≤n+2(n+1)+(n+2)=4n+4(3)
egyenlőtlenség. Ha n=1, és b=1, akkor (2) szerint N<8; ha b=2, akkor az a1=3, a2=1 választással kapjuk (2)-ből, hogy N<9; ha pedig b=3, akkor 1, 2 A-beli, és két újabb esetet kell megkülönböztetnünk aszerint, hogy a 4 A-hoz tartozik-e vagy B-hez. Ha 4∈A, akkor 5∈B, 6∈B, 7∈B, 8∈A és a 9 már nem osztályozható. Ha 4∈B, akkor 7∈A, 6∈B, 5∈B, és már a 8 sem osztályozható. Tehát n=1 mellett (3) helyett csak a kevesebbet mondó
N≤4n+4(3*)
állítható.
Meg kell még vizsgálnunk azt az esetet, amikor az n, n+1, n+2 számok ugyanabba az osztályba kerülnek. Válasszuk ebben az esetben az n-t tartalmazó osztályt A-nak. Mivel n∈A, n+1∈A, a 2n+1 szám csak B-beli lehet, így alkalmazhatjuk (2)-t az a1=n, a2=n+2, n=2n+1 helyettesítéssel:
N<2n+(n+2)+2n+1=5n+3.(4)
Ha n=1, akkor (4) szigorúbb (3*)-nál, tehát a legnagyobb N-et a már vizsgált
A={1,2,4,8},B={3,5,6,7}
osztályozás biztosítja. Ha n>1, akkor (3) szigorúbb (4)-nél, tehát N legnagyobb szóba jöhető értéke
Nmax=5n+2.(5)
Ez el is érthető, ha B-nek a
B={2n+1,2n+2,...,4n+2}
halmazt választjuk, A-nak pedig ennek komplementerét:
A={n,n+1,...,2n,4n+3,4n+4,...,5n+2}.

Kaptuk tehát, hogy N legnagyobb értékét (5) adja meg, kivéve az n=1 esetet, amikor Nmax=8.
 

  Seress Ákos (Budapest, Fazekas M. Gyak. Gimn., II. o. t.)
 

Megjegyzés. Az, hogy a kívánt osztályozás nem végezhető el tetszőlegesen nagy N-re, már abból látszik, hogy ha a1, a2∈A, b∈B, akkor a1+b∈B. Ha ugyanis most b mellé veszünk fel egy b1∈B elemet, azt is beláthatjuk, hogy a1+b∈A, szóval a baj ott kezdődik, hogy nem lehet eldönteni, hogy egy A-beli és egy B-beli elem összege hova tartozzon.
\epsfbox{1975-155-1.eps}{P. 221.}