Feladat:	Pontversenyen kívüli P.216	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Bajusz Ferenc ,  Borsodi Donát ,  Gombos János ,  Kecskés László ,  Kiss Emil ,  Páles Zsolt ,  Soukup Lajos
Füzet:	1975/december, 218. oldal		PDF  |  MathML
Témakör(ök):	Egyenlőtlenségek, Paralelepipedon, Térfogat, Szélsőérték-feladatok differenciálszámítás nélkül, Térgeometriai számítások trigonometria nélkül, Tetraéderek, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1974/május: Pontversenyen kívüli P.216

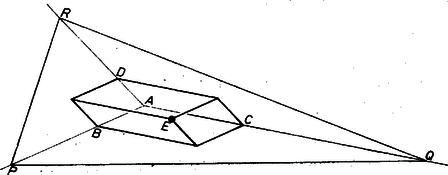
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Az iskolai függvénytáblázat képlettárában megtalálható összefüggés szerint az $APQR$ tetraéder $V$ térfogata $\begin{array}{c}{\displaystyle V=\frac{1}{6}\cdot AP\cdot AR\cdot AQ\cdot \text{sin}\left(AP\mathrm{,}AQ\right)\sphericalangle \cdot \text{sin}\delta \mathrm{,}}\end{array}$ ahol $\delta$ az $APQ$ sík és az $AR$ él hajlásszöge. Mivel $\left(AP\mathrm{,}AQ\right)\sphericalangle$ és $\delta$ adottak, $V$ akkor és csak akkor minimális, ha $AP\cdot AR\cdot AQ$ minimális. A Geometriai Feladatok Gyűjteménye I. kötetének 1991. feladatát esetünkre alkalmazva: $\begin{array}{c}{\displaystyle \frac{AB}{AP}+\frac{AC}{AQ}+\frac{AD}{AR}=1.}\end{array}$ (1) A számtani és mértani közepek közti összefüggés alapján: $\begin{array}{c}{\displaystyle \frac{1}{3}=\frac{\frac{AB}{AP}+\frac{AC}{AQ}+\frac{AD}{AR}}{3}\geqq \sqrt[3]{\frac{AB\cdot AC\cdot AD}{AP\cdot AQ\cdot AR}}\mathrm{,}}\end{array}$ (2) ahonnan $\begin{array}{c}{\displaystyle AP\cdot AQ\cdot AR\geqq 27AB\cdot AC\cdot AD\mathrm{.}}\end{array}$ (3) (2) és (3) ekvivalensek, (3) jobb oldala állandó, ezért $AP\cdot AQ\cdot AR$, és így $V$ is, akkor és csak akkor maximális, ha (2)-ben is egyenlőség van, azaz ha $\begin{array}{c}{\displaystyle \frac{AB}{AP}=\frac{AC}{AQ}=\frac{AC}{AR}=\frac{1}{3}\mathrm{,}}\end{array}$ hiszen összegük (1) szerint $1$. Megjegyezzük, hogy (1) azt is biztosítja, hogy az $AP=3AB$, $AQ=3AC$, $AR=3AD$ összefüggéseknek megfelelő $P$, $Q$, $R$ pontok, valamint $E$ egy síkban legyenek.     Gombos János (Miskolc, Földes F. Gimn.)