Kezdőlap


Feladat:	Pontversenyen kívüli P.215	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Kecskés Csaba , Kiss Emil , Páles Zsolt
Füzet:	1975/december, 217. oldal		PDF \| MathML
Témakör(ök):	Függvények folytonossága, Függvények, Négyzetek, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1974/május: Pontversenyen kívüli P.215

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egy konvex alakzat támaszegyenesének olyan egyenest nevezünk, melynek van közös pontja az alakzattal, s az alakzat minden pontja az egyenes egyik partján helyezkedik el. Bármely korlátos, konvex alakzatnak létezik tetszőleges irányú támaszegyenese, mégpedig kettő.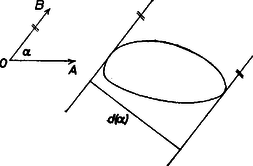
Vegyünk fel a síkban egy $O$ pontot és egy $\vec{O A} = i$ vektort. Értelmezzük a következő $d (α)$ függvényt. $\vec{O A}$ -t forgassuk el a szöggel (pozitív vagy negatív irányban $α$ előjelének megfelelően), kapjuk $\vec{O B}$ -t. Húzzuk meg az alakzat $\vec{O B}$ -vel párhuzamos két támaszegyenesét. Ezek távolságát jelöljük $d (α)$ -val.

E függvény definíciója szerint

d (α) = d (α + π)

. Belátható, hogy a

d (α)

függvény folytonos, ezért az

\begin{matrix} f (α) = d (α) - d (α + \frac{π}{2}) \end{matrix}

függvény is folytonos.

\begin{matrix} f (0) & = d (0) - d (\frac{π}{2}), f (\frac{π}{2}) = d (\frac{π}{2}) - d (π) = & (1) \\ = d (\frac{π}{2}) - d (0) . \end{matrix}

f (0) = f (\frac{π}{2}) = 0

, azaz

d (0) = d (\frac{π}{2})

, akkor a

0

és

\frac{π}{2}

radiánokhoz tartozó támaszegyenesek távolsága megegyezik, s ezért ezek négyzetet alkotnak.
Ha

f (0) \neq f (\frac{π}{2})

, akkor (1) miatt a

0

-hoz és

\frac{π}{2}

-hez tartozó függvényértékek ellenkező előjelűek, s így létezik olyan

0 < α_{0} < \frac{π}{2}

szög, melyre

f (α_{0}) = 0

. Erre az

α_{0}

-ra

d (α_{0}) = d (α_{0} + \frac{π}{2})

tehát az

α_{0}

irányú, és a rá merőleges támaszegyenesek négyzetet határoznak meg.

Kecskés Csaba (Budapest, Móricz Zs. Gimn., IV. o. t.)