|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Helyezkedjék el az oldalú és az oldalú négyzet egy négyzetben úgy, hogy ne legyen közös belső pontjuk. Ekkor van olyan egyenes, amelynek és ellenkező oldalán fekszik. Ha párhuzamos valamelyik oldalával, akkor két téglalapra bontja azt, és mindegyiknek az -re merőleges oldala legalább akkora, mint a sávban fekvő négyzet oldala. Ez esetben tehát oldala legalább akkora, mint és oldalának összege.
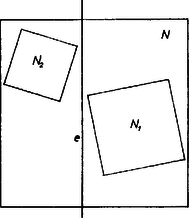 1. ábra
Ha metszi mindegyik oldalegyenesét, akkor vegyük mindkét oldalán -nek a tőle legtávolabbi , ill. csúcsát. A -en, ill. -n átmenő oldalegyenesek -vel egy , ill. derékszögű háromszöget alkotnak, amelyik -et, ill. -t tartalmazza. Állításunk bizonyítására elég azt megmutatni, hogy egy derékszögű háromszög tartalmazta négyzetek közül az a legnagyobb, amelyiknek két oldala a háromszög befogóin nyugszik, egy csúcsa pedig az átfogón van.
Valóban, ha ez igaz, akkor a -ben és -ben elhelyezhető legnagyobb négyzet átlója, -nek a átlójára esik, és mivel a négyzetek nem fedhetik át egymást, így átlóik összege átlóját, oldalhosszaik összege tehát oldalát adja, vagyis igaz a bizonyítandó állítás is.
A továbbiakban a fent megfogalmazott segédtételt bizonyítjuk.
Az derékszögű háromszögben levő tetszés szerinti négyzetet elmozgathatjuk úgy, hogy két csúcsa, mondjuk és az , ill. befogón legyen ‐ ha nem lett volna így eredetileg ‐, majd -ből nagyítva, ha kell, elérhetjük, hogy egy csúcs az átfogóra kerüljön. Elég tehát az ilyen helyzetű négyzeteket vizsgálni. Ezek középpontja a háromszög derékszögének szögfelezőjén van. Forgassuk el ugyanis a négyzetet a középpontja körül derékszöggel úgy, hogy az -n levő csúcsa a -n levőbe menjen át. Ekkor az egyenes is átmegy -be, így a középpont e két egyenestől egyenlő távolságban van, tehát rajta van a köztük levő szög felezőjén.
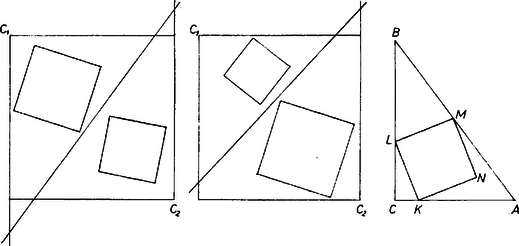 2. ábra
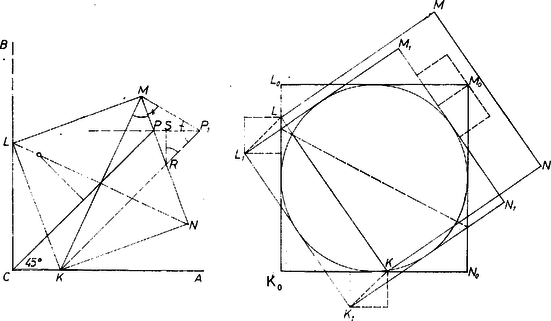 3. ábra
Annak a négyzetnek, amelyiknek az egyik csúcsa -be esik, az ezzel szemközti csúcsa nincs közelebb -hez, mint a -ből induló szögfelező -nel való metszéspontja. Elég tehát megmutatnunk, hogy ha és különbözik -től, akkor .
Toljuk el -t párhuzamosan a helyzetbe, ekkor a háromszög két oldalát kell összehasonlítanunk. Ezt a velük szemben levő szögek közvetítésével fogjuk megtenni. A -mel, ill. -gyel szemközti szög -gel, ill. -gel nagyobb -nál.
Jelöljük és metszéspontját -rel, vetülete -en legyen . háromszög derékszögű és egyenlő szárú, továbbá a és pont közt van, így amiből következik, hogy
Azt is tudjuk, hogy felezi -et, így felezi -t is, mert és párhuzamos. Ezért | |
De ekkor egyszersmind | |
amiből viszont következik, és ezt akartuk bizonyítani.
Megjegyzés. Gyorsabban befejezhetjük a bizonyítást a kerületi szögek tételének felhasználásával: , , és egy körön van, mert -os szögben látszik -ből is, -ből is. A kör középpontja a és húr felező merőlegesének metszéspontja. Mivel az előbbi húr átmegy az utóbbi felezőpontján, a húrok középponttól mért távolságai egy derékszögű háromszög befogója és átfogója. A húrtól mért távolság az átfogó, tehát a nagyobbik, így a húr a kisebb.
II. megoldás. Azt mutatjuk meg, hogy ha egy négyzetet egy olyan helyzetbe mozdítunk el a síkban, hogy és csúcsa a , ill. félegyenesen maradjon, akkor tartalmazni fogja az csúcsot. Ez valóban azt jelenti, hogy ha benne van egy derékszögű háromszögben, amelyiknek derékszöge az , akkor írható a háromszögbe -nél nagyobb négyzet, amelyiknek két oldala a befogókon nyugszik.
Forgassuk először el a négyzetet a középpontja körül körüljárásával ellentétes irányba hegyes szöggel, a helyzetbe, majd toljuk el a végleges helyére. és egyenlő távol van megfelelő oldalától a forgatás következtében. Rajzoljunk olyan négyzeteket, amelyeknek egyik csúcsa , ill. , másik két csúcsa legközelebbi oldalán van és -ből, ill. -ből induló átlója -lal párhuzamos. Ekkor a kérdéses átlók egyenlők lesznek, így megadják a kívánt eltolás vektorát.
Azt kell még belátnunk, hogy az eltolás hossza nagyobb, mint a szakasz -en túlnyúló darabja. Azonban távolsága -től ugyanakkora, mint -é -tól, mert és , továbbá és a két négyzet közös beírt körének egymással átellenes érintőpárjai, így metszéspontjaik összekötő egyenesére tükrözve a két négyzetet egymásba mennek át. Rajzoljuk meg azokat a négyzeteket, amelyeknek egyik csúcsa és két-két csúcsuk -en van, ezek egyike tartalmazza a kérdéses szakaszt, az tehát nem nagyobb, mint a négyzet átlója, aminek hossza viszont éppen az eltolás hossza. Ezzel ismét igazoltuk a segédtétel állítását.
Megjegyzés. A bizonyításban nem használtuk ki, hogy a nagy négyzetben tartalmazott két négyzet oldalának hossza és egység, így a b) részben azt bizonyítottuk be, hogy ha egy négyzetben elhelyezhető egy és négyzet úgy, hogy ne legyen közös belső pontjuk, akkor oldalának hossza legalább akkora, mint és oldalhosszának az összege. Ez lényegében megegyezik a P. 208. pontversenyen kívüli problémával, így a fentiekben annak is megoldását adtuk.
Lásd KÖMAL 48. kötet 3. szám 126. oldal. |
 PDF |
PDF |  MathML
MathML 

