Kezdőlap


Feladat:	Pontversenyen kívüli P.206	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Kiss Emil , Lelkes András , Páles Zsolt , Pócsi György
Füzet:	1975/április, 166 - 168. oldal		PDF \| MathML
Témakör(ök):	Trigonometria, Háromszögek nevezetes tételei, Körülírt kör, Kör egyenlete, Kör (és részhalmaza), mint mértani hely, Terület, felszín, Parabola, mint mértani hely, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1974/március: Pontversenyen kívüli P.206

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás. Először belátjuk, hogy az $A$ pont hozzátartozik a mértani helyhez, vagyis hogy

\begin{matrix} A B^{2} \cdot sin 2 β + A C^{2} \cdot sin 2 γ = 4 t . \end{matrix}

Ekvivalens átalakításokat végezve:

\begin{matrix} A B^{2} \cdot 2 sin β \cdot cos β + A C^{2} \cdot 2 sin γ cos γ = 4 \cdot \frac{A B \cdot A C sin α}{2}, \\ \frac{A B}{A C} \cdot sin β cos β + \frac{A C}{A B} sin γ cos γ = sin α, \\ sin γ cos β + cos γ sin β = sin α, \\ sin (β + γ) = sin α, \end{matrix}

amiről viszont tudjuk, hogy érvényes, hiszen

α = 180^{\circ} - (β + γ)

.
Hasonlóan kaphatjuk, hogy

B

és

C

pont szintén hozzátartozik a mértani helyhez.
A feladat további részét koordinátageometriai úton oldjuk meg.
Legyenek a háromszög csúcsai

A

(a_{1}; a_{2})

B

(b_{1}; b_{2})

C

(c_{1}; c_{2})

P

pont koordinátái pedig

x

és

y

. A feltétel szerint tehát:

\begin{matrix} sin 2 α {[(x - a_{1})}^{2} + {(y - a_{2})}^{2}] + sin 2 β {[(x - b_{1})}^{2} + {(y - b_{2})}^{2}] + & (1) \\ sin 2 γ {[(x - c_{1})}^{2} + {(y - c_{2})}^{2}] = 4 t . \end{matrix}

Mivel

α

β

γ

és

t

állandók, ez az egyenlet ilyen alakra hozható (ekvivalens átalakítások után):

\begin{matrix} A x^{2} + A y^{2} + B x + C y + D = 0. \end{matrix}

(2)

Tudjuk, hogy a (2) egyenletet vagy csak egy pont elégíti ki, vagy egy kör pontjai elégítik ki, vagy pedig semmilyen pont nem elégíti ki.
Mivel azonban

A

B

és

C

pontok kielégítik (2)-t, ezért (2) egy kör egyenlete.
(1) és (2) ekvivalenciája miatt tehát a keresett

P

pontok mértani helye a háromszög köré írt kör.

Páles Zsolt (Sátoraljaújhely, Kossuth L. Gimn. )

II. Megoldás. Bármilyen

A B C

háromszögre érvényes a

\begin{matrix} 4 T = 2 r^{2} (sin 2 α + sin 2 β + sin 2 γ) \end{matrix}

(3)

összefüggés.

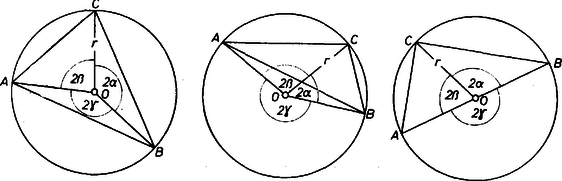Ugyanis ‐ rendre a hegyes, tompa és derékszögű háromszögre ‐

\begin{matrix} T = T (A O B) + T (B O C) + T (C O A) = \frac{1}{2} r^{2} sin 2 β + \frac{1}{2} r^{2} sin 2 γ + \frac{1}{2} r^{2} sin α, \\ T = T (A O C) + T (C O B) - T (A O B) = \frac{1}{2} r^{2} sin 2 β + \frac{1}{2} r^{2} sin 2 α - \frac{1}{2} r^{2} sin (360^{\circ} - 2 γ), \\ T = T (A O C) + T (B O C) = \frac{1}{2} r^{2} sin 2 α + \frac{1}{2} r^{2} sin 2 β . \end{matrix}

Ezek mindegyike viszont egyenlő az elsővel, hiszen

sin (360^{\circ} - 2 α) = - sin 2 α

és

sin 2 \cdot 90^{\circ} = 0

. Az első összefüggésből (3) nyilvánvaló.
Legyen

P O = d

A O P ∢ = ε

A O B ∢ = 2 γ

B O C ∢ = 2 α

és

C O A ∢ = 2 β

a szögek mindegyike irányított.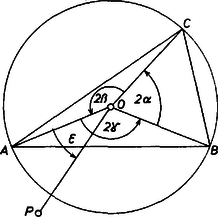

Ekkor a

\begin{matrix} P A^{2} = r^{2} + d^{2} - 2 r d cos ε, \\ P B^{2} = r^{2} + d^{2} - 2 r d cos (2 γ - ε), \\ P C^{2} = r^{2} + d^{2} - 2 r d cos (2 β + ε) \end{matrix}

összefüggések alapján:

\begin{matrix} P A^{2} \cdot sin 2 α + P B^{2} sin 2 β + P C^{2} sin 2 γ = \\ = (r^{2} + d^{2}) (sin 2 α + sin 2 β + sin 2 γ) - 2 r d (cos ε sin 2 α + cos (2 γ - ε) sin 2 β + cos (2 β + ε) sin 2 γ), \end{matrix}

2 r d

szorzótényezőjét alakítva:

\begin{matrix} cos ε sin 2 α + cos 2 γ cos ε sin 2 β + sin 2 γ sin ε sin 2 β + cos 2 β \cdot cos ε \cdot sin 2 γ - \\ sin 2 β sin ε \cdot sin 2 γ = cos ε (sin 2 α + cos 2 γ sin 2 β + cos 2 β sin 2 γ) = \\ cos ε (sin 2 α + sin (2 β + 2 γ)) = cos ε (sin 2 α + sin (360^{\circ} - 2 α)) = cos ε (sin 2 α - sin 2 α) = 0. \end{matrix}

Azt kaptuk tehát, hogy

\begin{matrix} P A^{2} sin 2 α + P B^{2} sin 2 β + P C^{2} sin 2 γ = (r^{2} + d^{2}) (sin 2 α + sin 2 β + sin 2 γ), \end{matrix}

(a sík minden P pontjára). Ezt és (3)-at összevetve, a kérdés így tehető fel: mi azon

P

pontok mértani helye, amelyekre

(r^{2} + d^{2})

(sin 2 α + sin 2 β + sin 2 γ) = 2 r^{2} (sin 2 α + sin 2 β + sin 2 γ)

, vagyis:

\begin{matrix} (r^{2} - d^{2}) (sin 2 α + sin 2 β + sin 2 γ) = 0. \end{matrix}

Mivel sin

2 α + sin 2 β + sin 2 γ \neq 0

, ezért

r^{2} - d^{2} = 0

, vagyis a mértani hely a háromszög köré írható kör.
(

sin 2 α + sin 2 β + sin 2 γ

azért nem lehet nulla, mert

4 T = 2 r^{2} (sin 2 α + sin 2 β + + sin 2 γ) > 0)

Kiss Emil (Budapest, Fazekas M. Gyak Gimn. )