Kezdőlap


Feladat:	Pontversenyen kívüli P.205	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Bérczy Tamás , Czompó József , Kiss Emil , Lelkes András , Páles Zsolt , Pócsi György , Veres Sándor
Füzet:	1975/október, 73 - 75. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Térfogat, Térgeometriai bizonyítások, Tetraéderek, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1974/március: Pontversenyen kívüli P.205

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az $A B C D$ tetraéder térfogatát $V_{A B C D}$ -vel jelöljük. Analóg jelölésmódot vezetünk be más tetraéderek térfogatára is.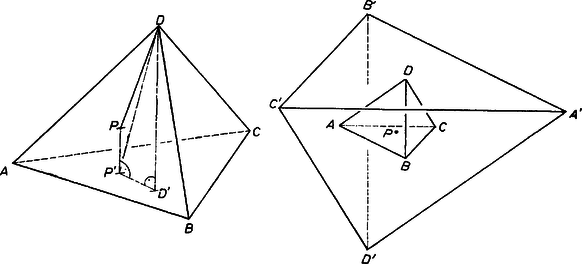
Vetítsük $D$ -t, ill. $P$ -t az $A B C$ háromszög síkjára, a vetületek legyenek $P'$ , ill. $D'$ .

A háromszög-egyenlőtlenség szerint

\begin{matrix} D P' \leq D P + P P', \end{matrix}

továbbá, mivel

D D'

merőleges az

A B C

háromszög síkjára:

D P' \geq D D'

. A fentiek miatt

\begin{matrix} D D' \leq D P + P P' . \end{matrix}

Az egyenlőtlenség mindkét oldalát a pozitív

T_{A B C} / 3

-mal megszorozva, figyelembe véve a térfogatképletet, a

\begin{matrix} V_{A B C D} \leq V_{A B C P} + \frac{1}{3} T_{A B C} \cdot P D \end{matrix}

egyenlőtlenséghez jutunk.
Hasonló módszerrel kaphatjuk meg a

\begin{matrix} V_{A B C D} & \leq V_{A B D P} + \frac{1}{3} T_{A B D} \cdot P C, \\ V_{A B C D} & \leq V_{A C D P} + \frac{1}{3} T_{A C D} \cdot P B, \\ V_{A B C D} & \leq V_{B C D P} + \frac{1}{3} T_{B C D} \cdot P A \end{matrix}

egyenlőtlenségeket. Mivel

P

a tetraéder belsejében van:

V_{A B C D} = V_{A B C P} + V_{A B D P} + V_{A C D P} + V_{B C D P}

. Ezt figyelembe véve a négy egyenlőtlenség összeadásával a

\begin{matrix} 4 V_{A B C D} \leq V_{A B C D} + \frac{1}{3} (T_{A B C} \cdot P D + T_{A B D} \cdot P C + T_{A C D} \cdot P B + T_{B C D} \cdot P A) \end{matrix}

egyenlőtlenséget nyerjük. Ebből átrendezéssel adódik az állítás.
Belátható, hogy egyenlőség akkor és csak akkor lehetséges, ha a tetraédernek van magasságpontja és az

P

-vel egybeesik.

Czompó József (Győr, Révai M. Gimn.)

II. megoldás. Tekintsük azt a tetraédert, amelynek lapjai párhuzamosak az eredeti

A B C D

tetraéder lapjaival és átmennek a szemben levő csúcson. Ez a tetraéder hasonló az eredetihez, és a hasonlóság aránya 1:3. Ezért

\begin{matrix} V' = 27 V; T_{B' C' D'} & = 9 T_{B C D}; T_{A' B' C'} = 9 T_{A B C}; & (1) \\ T_{A' B' D'} & = 9 T_{A B D}; T_{A' C' D'} = 9 T_{A C D} . \end{matrix}

P

-nek az

A' B' C', A' C' D', A' B' D', B' C' D'

lapoktól mért távolságát jelölje

m_{D}

m_{B}

m_{C}

, ill.

m_{A}

. Nyilván

\begin{matrix} P A \geq m_{A}, P B \geq m_{B}, P C \geq m_{C}, P D \geq m_{D}, \end{matrix}

(2)

emiatt

\begin{matrix} V' \leq \frac{1}{3} T_{A' B' C'} \cdot P D + T_{A' B' D'} \cdot P C + T_{A' C' D'} \cdot P B + T_{B' C' D'} \cdot P A . \end{matrix}

(1)-et behelyettesítve

\begin{matrix} 27 V \leq \frac{1}{3} (9 T_{A B C} \cdot P D + 9 T_{A B D} \cdot P C + 9 T_{A C D} \cdot P B + 9 T_{B C D} \cdot P A) . \end{matrix}

Ennek átrendezése után bizonyítandó állításunkat kapjuk.
(2)-ből az is kiderül, hogy egyenlőség akkor és csak akkor van, ha a tetraédernek van magasságpontja és éppen

P

az.