Feladat:	Pontversenyen kívüli P.193	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Lakner Péter ,  Lelkes András ,  Páles Zsolt ,  Rapp Ferenc
Füzet:	1975/március, 120 - 121. oldal		PDF  |  MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Vektorok lineáris kombinációi, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1973/december: Pontversenyen kívüli P.193

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. $\begin{array}{c}{\displaystyle |{\overrightarrow{OP}}_1+{\overrightarrow{OP}}_2+\text{...}+{\overrightarrow{OP}}_n|\geqq \mathrm{1,}}\end{array}$ (1) Jelöljük $F$-fel azt az $e$ által határolt félsíkot, amelyben a $P_i$ pontok vannak, és válasszuk az $e$-vel megegyező állású egységvektorok közül $\text{e}$-nek azt, amelyiket ${180}^{\circ }$-nál kisebb pozitív irányú forgatás visz $F$-be.     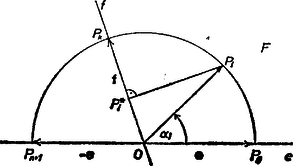Legyen $P_0$ az a pont, melyre $\overrightarrow{O{P}_0}=\text{e}$, és $P_{n+1}$ a $P_0$ $O$-ra vonatkozó tükörképe. Jelöljük az $\text{e}$-t $O{P}_i$-be vivő forgatást ${\alpha }_i$-vel, és tegyük fel, hogy a $P_i$ pontok úgy vannak megszámozva, hogy az ${\alpha }_i$ sorozat monoton nő: $\begin{array}{c}{\displaystyle 0\le {\alpha }_0\le {\alpha }_1\le \text{...}\le {\alpha }_n\le {\alpha }_{n+1}={180}^{\circ }\mathrm{.}}\end{array}$ (2) (Ha ez nem teljesülne, változtassuk meg a $P_i$ pontok számozását úgy, hogy az új számozás mellett már teljesüljön (2). Ezt mindig megtehetjük, hiszen ez a módosítás a (1)-ben szereplő összeget változatlanul hagyja.) Feltevésünk szerint $n$ páratlan, mondjuk $n=2k-1$. Jelöljük $f$-fel az $O{P}_k$ egyenest, $\text{f}$-fel az $\overrightarrow{O{P}_k}$ vektort, és $P_i^{*}$-gal a $P_i$ pont $f$-en levő vetületét. Azt fogjuk belátni, hogy $\begin{array}{c}{\displaystyle |\overrightarrow{O{P}_1^{*}}+\text{...}+\overrightarrow{O{P}_n^{*}}|\ge 1\mathrm{,}}\end{array}$ (3) ebből már következik (1), hiszen a $\overrightarrow{P^{*}{P}_i}$, vektorok merőlegesek $\text{f}$-re, így $\text{f}$-re merőleges az összegük is, és Pithagorasz tétele szerint ${\displaystyle \begin{array}{c}\hfill {\displaystyle |\overrightarrow{O{P}_1}+\text{...}+\overrightarrow{O{P}_n}{|}^2=|\overrightarrow{O{P}_1^{*}}+\text{...}+\overrightarrow{O{P}_n^{*}}{|}^2+|\overrightarrow{P_1^{*}{P}_1}+\text{...}+\overrightarrow{P_n^{*}{P}_n}{|}^2\ge }\hfill \\ \hfill {\displaystyle \ge |\overrightarrow{O{P}_1^{*}}+\text{...}+\overrightarrow{O{P}_n^{*}}{|}^2\mathrm{.}}\hfill \end{array}}$ Mivel $\overrightarrow{O{P}_i^{*}}$ egyállású $\text{f}$-fel, van olyan ${\lambda }_i$ szakasz, amelyre $\overrightarrow{O{P}_i^{*}}={\lambda }_i\text{f}$. Elég belátnunk, hogy $\begin{array}{c}{\displaystyle {\lambda }_1+\text{...}+{\lambda }_n\ge 1\mathrm{,}}\end{array}$ (4) ami valóban igaz, mert ${\lambda }_i=\text{cos}\left({\alpha }_k-{\alpha }_i\right)$, és emiatt ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\lambda }_i\ge {\lambda }_0=\text{cos}{\alpha }_k\mathrm{,}\text{<span style="font-weight: normal;font-style: normal;">ha</span>}1\le i<k;}\hfill & \text{(<mn>5</mn>)}\\ \hfill {\displaystyle {\lambda }_i\ge {\lambda }_{n+1}=-\text{cos}{\alpha }_k\mathrm{,}\text{<span style="font-weight: normal;font-style: normal;">ha</span>}k<i\le n\mathrm{,}}\hfill & \text{(<mn>6</mn>)}\end{array}}$ hiszen $1\le i<k$ mellett $0\le {\alpha }_k-{\alpha }_i\le {\alpha }_k\le {180}^{\circ }$, és a $0\le x\le {180}^{\circ }$ szakaszon $\text{cos}x$ monoton fogy, ha pedig $k<i\le n$ akkor $-{180}^{\circ }\le {\alpha }_k-{180}^{\circ }\le {\alpha }_k-{\alpha }_i\le 0$, és a $-{180}^{\circ }\le x\le 0$ szakaszon $\text{cos}x$ monoton nő. Mármost (5) szerint $\begin{array}{c}{\displaystyle {\lambda }_1+\text{...}+{\lambda }_{k-1}\ge \left(k-1\right){\lambda }_0\mathrm{,}}\end{array}$ (7) és (6). szerint $\begin{array}{c}{\displaystyle {\lambda }_{k+1}+\text{...}+{\lambda }_n\ge \left(k-1\right){\lambda }_{n+1}\mathrm{,}}\end{array}$ (8) tehát $\begin{array}{c}{\displaystyle \left({\lambda }_1+\text{...}+{\lambda }_{k-1}\right)+\left({\lambda }_{k+1}+\text{...}+{\lambda }_n\right)\ge \left(k-1\right)\left({\lambda }_0+{\lambda }_{n+1}\right)=\mathrm{0,}}\end{array}$ (9) amiből következik (4), hiszen ${\lambda }_k=1$.   Megjegyzés. Ha $n=1$, (1) és (4) nyilvánvaló, az (5)‐(9) állítások pedig formálisan ugyan helyesek, de semmitmondóak. (7)-ből és (8)-ból kiolvasható, hogy (1)-ben az egyenlőség jele akkor és csakis akkor teljesül, ha $P_1=\text{...}=P_{k-1}=P_0$ és $P_{k+1}=\text{...}=P_n=P_{n+1}$ (és $P_k$ tetszőleges).