| Feladat: | Pontversenyen kívüli P.192 | Korcsoport: 18- | Nehézségi fok: - |
| Megoldó(k): | Páles Zsolt | ||
| Füzet: | 1974/április, 170 - 171. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Beírt gömb, Térgeometriai bizonyítások, Térgeometria alapjai, Pontversenyen kívüli probléma | ||
| Hivatkozás(ok): | Feladatok: 1973/november: Pontversenyen kívüli P.192 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Nevezzük az eredeti konvex poliéder lapjait régi lapoknak. Indirekt módon okoskodunk, azaz feltesszük: van olyan poliéder és annak a leírt módon való csonkolása, hogy a keletkező új poliéderbe lehet gömböt írni. Ez azt is jelenti, hogy már a kiindulási poliédernek van beírt gömbje. Fessük a régi lapokat fehérre, az új lapokat feketére. Tekintsük az új poliéder minden lapján a beírt gömb érintési pontját és a lapokon azokat a háromszögeket, amelyeknek csúcsai az említett érintési pontok, alapjai pedig a fekete lapok egy‐egy éle. Ekkor a fekete lapok kivétel nélkül ilyen háromszögekre bomlanak, a fehér lapokon azonban más háromszögek is keletkeznek. Mivel feltevésünk szerint a fekete lapok sehol sem érintkeznek egymással, azért minden fehér lapon az olyan élek, amelyekben fehér lap fekete lappal fut össze, váltakoznak olyan élekkel, amelyekben fehér lap fehér lappal szomszédos. 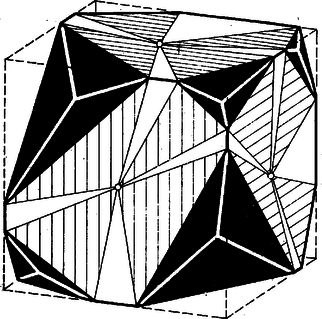 1. ábra A vizsgált fekete és fehér háromszögek közül a közös alapúak egybevágók, hiszen síkjaik érintősíkjai a beírt gömbnek, egymás tükrös párjai a közös élükön és a gömb középpontján átmenő síkra nézve. Tekintsük a vizsgált összes fehér, valamint az összes fekete háromszögekben az érintési pontokban fekvő szögek összegét. A fehér háromszögek ezen csúcsainál fekvő szögek összege egyenlő a fekete háromszögek ezen csúcsainál fekvő szögek összegével. A mondottak szerint ez az összeg a fekete háromszögek esetében éppen egyenlő a fekete lapok számának -szeresével, a fehérek esetében viszont kisebb a fehér lapok számának -szeresénél, hiszen a fehér lapoknak az érintési pontokban fekvő szögei nem fedik be az egész síkot e körül a pont körül, vagyis . Ez viszont ellentmondásban van kiindulásunkkal, hiszen fekete lapunk annyi van, ahány csúcsa volt az eredeti poliédernek, tehát . ‐ Ezzel a feladat állítását bebizonyítottuk. Páles Zsolt (Sátoraljaújhely) Megjegyzések. 1. Az 1. ábra kockából kiindulva kívánja segíteni a gondolatmenet követését. Ne felejtsük azonban, hogy bizonyításunk szerint a fekete lapok nem érinthetik mind a beírt gömböt, tehát ezek tekintetében nem mérethű az ábra. (Csak az előlap bal felső és jobb alsó csúcsát lemetsző sík érint.) 2. Arra viszont, hogy esetére az állítás nem mindig érvényes, példa a szabályos oktaédernek az a lecsonkolása, melyben minden csúcs környezetének lemetsző síkja merőleges a csúcsot a középponttal összekötni tengelyre és érinti az oktaéder ‐ beírt gömbjét ‐ mert az oktaéderbe beírt gömb sugara nagyobb, mint a körülírt gömb sugarának a fele (2. ábra). 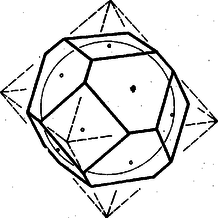 2. ábra Ugyanilyen példa a szabályos ikozaéder is. |