Kezdőlap


Feladat:	Pontversenyen kívüli P.184	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Csuka Gábor , Kiss Emil , Veres Sándor
Füzet:	1974/október, 72 - 75. oldal		PDF \| MathML
Témakör(ök):	Elsőfokú (és arra visszavezethető) egyenletrendszerek, Kocka, Tér parkettázás, Szabályos sokszögek által határolt testek, Térgeometriai bizonyítások, Vektorok lineáris kombinációi, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1973/szeptember: Pontversenyen kívüli P.184

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1. ábrán látható lest 7 egybevágó kockából áll: egy központi kockából és a hozzá a lapjain keresztül csatlakozó másik hat kockából.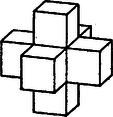

1. ábra

A tér kívánt kitöltését úgy készítjük el, hogy először egybevágó kockákkal töltjük ki a teret, majd ezeket hetes csoportokba szervezzük, a részeket mintegy utólag ragasztjuk össze, hogy a kívánt alakzatokat megkapjuk. Ennek érdekében természetesen olyan csoportokat alkothatunk, amelyekből az 1. ábra alakzata kialakul.
Töltsük ki tehát a teret az 1. ábrán látható testet alkotó kockákkal egybevágó kockákkal. Vegyünk e kockákból egy ,,vízszintes'' réteget, azaz vegyük ki közülük azokat, amelyek középpontjai az egyik olyan síkban vannak, amelyik párhuzamos a kockák valamelyik lapjával. Ebben az

S

síkban a kockák metszetei négyzetrácsot alkotnak. Az olyan csoportnak, amelynek a központi kockáját metszi az

S

sík, öt eleme van az

S

síkban, ezek metszete a 2. ábra alakzata.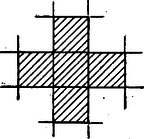

2. ábra

Ezeken kívül még azoknak a csoportoknak metszi valamelyik elemét

S

, amelyek központi eleme az

S

fölötti vagy az

S

alatti, a választott réteggel közvetlenül szomszédos rétegben vannak. Egy ilyen csoportnak egyetlen elemét metszi

S

, ezeket a metszeteket

F

-fel vagy

A

-val jelöljük aszerint, hogy a centrumuk

S

felett vagy alatt helyezkedik-e el. Az

S

-en levő négyzetrácsot tehát a 2. ábrán látható kereszt alakú

K

alakzatokkal, és

F

-fel és

A

-val jelölt négyzetekkel kell kitöltetnünk.
Várhatóan minden rétegben ugyanolyan sűrűn helyezkednek el a csoportcentrumok, emiatt e három alakzatot ugyanolyan sűrűn kell elhelyeznünk, ami most azt jelenti, hogy a sík elég nagy részeiben körülbelül ugyanannyi

K

-nak,

A

-nak és

F

-nek kell lennie. Azt is mondhatjuk, hogy mivel az 1. ábrán látott testtel egybevágó alakzatokban minden centrumot hat másik kocka övez, centrumul csak minden hetedik kockát célszerű választani. Legegyszerűbben úgy tehetünk ennek eleget, ha ez minden sorban teljesül. Vizsgáljuk meg tehát, hogy a 3. ábrán megkezdett rendszer folytatható-e először az

S

sík, majd az egész tér kívánt felbontásáig.

3. ábra

Nevezzük a most elhelyezett centrumok sorát elsőnek, és a felette levőt másodiknak. Ebben a másodikban is lesznek centrumok, mégpedig minden hatos közben (hat szomszédos üres, négyzetben) egy-egy centrum. Nem lehet centrum a hatos közök szélső eleme, mert ekkor a rá épülő

K

alakzat beleütközne a már elhelyezett

K

-ba, így csak a hatos közök szélétől számított második vagy harmadik négyzet lehet centrum. Legyen mondjuk a második négyzet a centrum (4. ábra).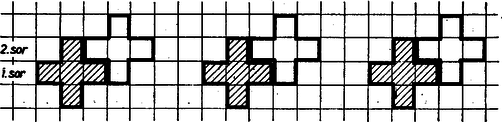

4. ábra

Ha ezt követően minden új sorban a hatos közökben balról számított második négyzetet választjuk centrumnak, az 5. ábra rendszeréhez jutunk.

5. ábra

Áttekinthetőség kedvéért csak a

C

centrumokat jelöltük, a csatlakozó négyzeteket pálcikák jelzik. Minden hatos blokkban két szabad hely van még, ezek lesznek felváltva az alulról, illetve felülről benyúló

A

, illetve

F

elemek. (Megfigyelhetjük, hogy az 5. ábrán függőlégesen elhelyezkedő hatos blokkokban a szélüktől számított 3. négyzet a centrum, ha tehát indításkor a 3. négyzetet választjuk centrumnak a 4. ábrán, akkor is lényegében erre a rendszerre jutunk.)
Az 5. ábra rendszere már kijelöli az

S

feletti réteg rendszerét is, legalábbis e rendszer centrumait és

A

-jait, hiszen az

S

-beli centrumok ebben a rétegben

A

-ba mennek át, így nyilván a hiányzó négyzetek lesznek az

F

-ek. Azt is mondhatjuk, hogy úgy kapjuk meg ezt a rendszert, hogy az 5. ábra rendszerét úgy toljuk el az 5. ábra síkjában, hogy a centrumok

A

-ba mennek át. Gondot okoz azonban, hogy az így kialakuló térbeli rendszert nehéz áttekinteni. Vizsgáljuk meg, hogy melyek lesznek azok a kockák a térben, amelyeket centrumul választunk. Válasszunk a jobb áttekintés kedvéért a térben olyan koordináta-rendszert, amelynek

x

-tengelye az 5. ábra vízszintes egyenese,

y

-tengelye az 5. ábra függőleges egyenese, egysége egy kis négyzet oldala, és origója az 5. ábra valamelyik centrumnégyzetének a középpontja. Az 5. ábrán minden centrumból újabb centrumot kapunk, ha az e

(7,0,0)

vagy az f

(2,1,0)

vektorral eltoljuk. Az 5. ábra síkjától a térbe kilépve újabb eltolást ad az 5. ábra centrumait az

F

-ek feletti centrumokba vivő g

(3,0,1)

eltolás. Azt várjuk tehát, hogy a térben azok a kockák lesznek centrumok, amelyek előállíthatók az origót tartalmazó kockából véges sok eltolás láncolatával, ha e láncolat minden eleme

\pm e, \pm f, \pm g

valamelyike. Azt is mondhatjuk, hogy azok a kockák lesznek centrumok, amelyek középpontjainak r

(x, y, z)

helyvektorai előállíthatók

\begin{matrix} r = k e + m f + n g \end{matrix}

alakban, ahol

k, m, n

egész számok. Ezt az egyenletet a vektorok koordinátáira átírva az

\begin{matrix} x = 7 k + 2 m + 3 n \\ y = m \\ z = n \end{matrix}

egyenletrendszert kapjuk, ami akkor és csakis akkor oldható meg az egész számok körében, ha

x, y, z

olyan egészek, amelyekre

x - 2 y - 3 z

osztható 7-tel.
Válasszuk tehát centrumoknak azokat a kockákat a térben, amelyek középpontjainak

x, y, z

koordinátáira az

(x - 2 y - 3 z)

kifejezés osztható 7-tel. Megmutatjuk, hogy a térben minden kocka vagy centrum, vagy egy ‐ és csakis egy centrummal szomszédos, azaz egy és csakis egy centrumnak választott kockával van közös oldallapja. Legyenek egy tetszőleges

K_{0}

kocka középpontjának a koordinátái

(x, y, z)

, és tekintsük az

N = x - 2 y - 3 z

számot. Ha

N

osztható 7-tel, a

K_{0}

kocka centrum. Ha ez 7-tel osztva 1-et vagy 6-ot ad. marhádékul, akkor az

(x - 1, y, z)

, ill. az

(x + 1, y, z)

pontot tartalmazó kocka centrum. Ha az

N : 7

osztás maradéka 2 vagy 5, akkor az

(x, y + 1, z)

(x, y - 1, z)

pontok adják a

K

-lal szomszédos centrum középpontját. Ha pedig a maradék 3 vagy 4, akkor

(x, y, z + 1)

, illetve

(x, y, z - 1)

a kívánt centrum. A választott csoportosítás helyességét ezzel bebizonyítottuk, a megoldást befejeztük.

Megjegyzések. 1. Előkészíthetjük a tér kitöltését az építőtest két modellével való rendszeres próbálgatással is (sőt esetleg csupán elképzeléssel). Jelöljük a test magjához ragasztott kockákat az

A

(alsó),

F

(felső),

E

(elülső),

H

(hátsó),

J

(jobb),

B

(bal) betűkkel és ugyanígy ezek lapjait is, pl, egy test elülső kockájának jobb oldali lapja

E J

.
A

T_{1}

építőtest

E J

lapjához a

T_{2}

testből illeszkedő kocka nyilvánvalóan a

J E

laphoz is illeszkedik. Pontosabban: az

E J

-hez illeszkedő lap

T_{2}

-nek valamilyen

X B

lapja lesz, ahol

X

F, A, B

és

H

kockák valamelyike. A fenti megoldásban az

F B

lap ez, és ekkor

T_{2}

-ből

F H

illeszkedik

T_{1}

-nek

J E

lapjához. Továbbá

T_{2}

-nek

B

és

H

kockája is 2‐2 lapjával illeszkedik

T_{1}

-hez: a

B F, B H, H F, H B

lap rendre

T_{1}

-nek

E A, A E, J A, A J

. lapjához, vagyis a két építőtest 6‐6 lapjával illeszkedik egymáshoz (6. ábra).

6. ábra

X

helyére

A

-t vége ennek az illeszkedésnek egy vízszintes síkon való tükörképét kapnánk.

X B

-ként

T_{2}

-nek

B B

lapját választva még á

B H

és a

H B

lap illeszkedik

T_{1}

-nek

J E, J J

lapjához, más illeszkedés ekkor nincs köztük (7. ábra).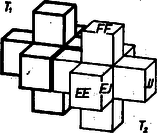

7. ábra

A 4. ábra szerinti csatlakozás ennek tükörképe egy az

E

lapokkal párhuzamos síkra. (

X = H

esetén, hasonlóan a 7. ábrabeli helyzetnek egy tükörképét kapnánk, ti. amikor

T_{1}

magjának azon az átlós síkján tükrözünk, amely átmegy az

E

és

J

kockák közös élén. Ezzel áttekintettük a

T_{1}

test

E J

lapjának minden illeszkedési lehetőségét.
Vegyük észre, hogy itt

T_{1}

-nek is,

T_{2}

-nek is 1‐1 külső, a konvex burkába tartozó ‐ mondjuk így: véglapja szerepel az illeszkedésben:

J J

, illetve

B B

; a további 2‐2 illeszkedés lapjait pedig kézenfekvő beugró lapoknak nevezni. A 6. ábra, szerinti ‐ szoros; 6‐6 lap menti ‐ illeszkedésben viszont mind a 6 illeszkedő lap beugró (két különböző nagybetűvel megjelölt) lap.
Mivel egy építőtestnek 6 véglapja van, kézenfekvő ebből az a sejtés, hogy a térkitöltésben ‐ ha ez lehetséges ‐

T_{1}

-hez 6 másik test illeszkedik a 7. ábra szerint, lazábban, 3‐3 lap mentén (természetesen alkalmas elfordításokkal értve az ábrát), ezzel

T_{1}

-nek

6 \cdot 3

lapjának illeszkedése intéződik el; a hátralevő

6 \cdot 5 - 6 \cdot 3 = 6 \cdot 2

lap már mind beugró lap, ezekhez pedig 2 másik építőtest ,,szorosan'' illeszkedik, tehát

T_{1}

-hez együttvéve 8 másik test illeszkedik.
Arról már könnyű meggyőződni, modellekkel (elég hozzá 3 példány), hogy

T_{1}

-nek ez a körülépítése valóban lehetséges, és ebből adódik az az újabb sejtés, hogy ezzel a tér kitöltési módja is egyértelműen meg van határozva. Ezt azonban természetesen még bizonyítani kell. Szoros illeszkedésben

\sqrt[]{3}

egység, a laza esetben pedig

\sqrt[]{5}

egység a két test centrumának távolsága.
2. Fjodorov (1880-ban) és H. Minkowski (1897-ben) orosz matematikusok megadták az összes ‐ lényegében különböző ‐ olyan konvex testet (poliédert), melyekkel a teret ki lehet tölteni.