Kezdőlap


Feladat:	Pontversenyen kívüli P.176	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Balázs Á. , Bara T. , Bíró B. , Buza A. , Fukker B. , Homonnay G. , Horváth Mária , Jakab Tibor , Kelemen Dezső , Kiss E. , Kollár János , Kovács Sándor , Kovács Zoltán , Markó P. , Páles Zs. , Pálffy L. , Rapp Ferenc , Timár J. , Vörös Z.
Füzet:	1974/március, 121 - 122. oldal		PDF \| MathML
Témakör(ök):	Racionális számok és tulajdonságaik, Irracionális számok és tulajdonságaik, Pont körüli forgatás, Indirekt bizonyítási mód, Négyzetek, Háromszög-rácsok geometriája, Vektorok lineáris kombinációi, Vektorok felbontása összetevőkre, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1973/április: Pontversenyen kívüli P.176

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ismeretes ‐ ez könnyen be is látható ‐ a szabályos háromszög rács következő tulajdonsága: ha $A$ és $B$ rácspont, akkor $B$ -nek $A$ körüli $+ 60^{\circ}$ -os elforgatottja is rácspont. Ezt használjuk fel. Indirekt módon bizonyítunk. Tegyük fel, hogy az $A_{1}$ , $B_{1}$ , $C_{1}$ és $D_{1}$ rácspontok által meghatározott négyszög négyzet (a csúcsok körüljárása legyen pozitív). Jelölje $i = 1, 2, 3, ...$ mellett $A_{i + 1}$ , $B_{i + 1}$ $C_{i + 1}$ és $D_{i + 1}$ rendre $B_{i}$ -nek $A_{i}$ körüli, $C_{i}$ -nek $B_{i}$ körüli, $D_{i}$ -nek $C_{i}$ körüli és $A_{i}$ -nek $D_{i}$ körüli $+ 60^{\circ}$ -os elforgatottját. Az előbb mondottak értelmében a forgatásokkal kapott pontok mindegyike rácspont. $A_{i + 1}$ -nek az $A_{i} B_{i}$ egyenestől mért távolsága $\sqrt[]{3} \cdot A_{i} B_{i} / 2$ , tehát kisebb, mint $A_{i} B_{i}$ , ezért az $A_{i + 1}$ , $B_{i + 1}$ , $C_{i + 1}$ és $D_{i + 1}$ pontok mindegyike az $A_{i} B_{i} C_{i} D_{i}$ négyzet belsejében van (1. ábra).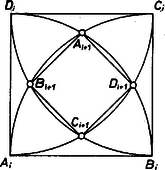

1. ábra

Ha az

A_{i} B_{i} C_{i} D_{i}

és

A_{i + 1} B_{i + 1} C_{i + 1} D_{i + 1}

négyszögeket

+ 90^{\circ}

-kal elforgatjuk az

A_{i} B_{i} C_{i} D_{i}

négyzet középpontja körül, az

A_{i + 1}

pont

B_{i + 1}

-be, a

B_{i + 1}

pont

C_{i + 1}

-be, a

C_{i + 1}

pont

D_{i + 1}

-be és a

D_{i + 1}

pont

A_{i + 1}

-be kerül, vagyis

A_{i + 1} B_{i + 1} C_{i + 1} D_{i + 1}

is négyzet. Így azt kaptuk, hogy az

A_{1} B_{1} C_{1} D_{1}

négyzet belsejében végtelen sok rácspont van, ez pedig ellentmondás.

Jakab Tibor (Budapest, Berzsenyi D. Gimn.)

II. megoldás. Ismét indirekt módon bizonyítunk.
A rácspontokból álló négyzet csúcsait (a pozitív körüljárás irányában haladva) jelölje

A

B

C

és

D

. Az adott rácsot meghatározó háromszöggel egybevágó

A X Y

pozitív körüljárású háromszög

A

csúcsában vegyük fel a koordináta-rendszer kezdőpontját, és az

A X

félegyenes legyen az

x

tengely pozitív fele (2. ábra).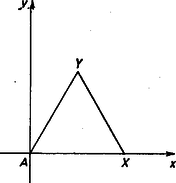

2. ábra

Mint ismeretes, azok és csak azok a

P

pontok lesznek rácspontok, amelyekre alkalmas

α

és

β

egész számokkal

\begin{matrix} \vec{A P} = α \cdot \vec{A X} + β \cdot \vec{A Y} . \end{matrix}

Ezért, s a feltevés alapján van olyan

p

q

r

s

egész szám, hogy

\begin{matrix} \vec{A B} = p \cdot \vec{A X} + q \cdot \vec{A Y}, \\ \vec{A D} = r \cdot \vec{A X} + s \cdot \vec{A Y} . \end{matrix}

Mivel másrészt

\vec{A X}

koordinátái

(1; 0)

és

\vec{A Y}

koordinátái

(\frac{1}{2}, \frac{\sqrt[]{3}}{2})

azért

\begin{matrix} \vec{A B} (p + \frac{q}{2}, \frac{q \sqrt[]{3}}{2}), \\ \vec{A D} (r + \frac{s}{2}, \frac{s \sqrt[]{3}}{2}) . \end{matrix}

A feltevés szerint

\vec{A D}

\vec{A B}

-nek

(+ 90^{\circ})

-os elforgatottja, ezért

\begin{matrix} p + \frac{q}{2} & = \frac{s \sqrt[]{3}}{2}, \\ - \frac{q \sqrt[]{3}}{2} & = r + \frac{s}{2} . \end{matrix}

Ezekből ellentmondás következik, hiszen pl.

\sqrt[]{3} = \frac{2 p + q}{s}

, vagyis

\sqrt[]{3}

racionális, ami nyilván nem igaz.

Kelemen Dezső (Kaposvár, Táncsics M. Gimn.)