Feladat: Pontversenyen kívüli P.164 Korcsoport: 18- Nehézségi fok: -
Megoldó(k):  Kiss Emil 
Füzet: 1974/március, 117 - 118. oldal  PDF  |  MathML 
Témakör(ök): Részhalmazok, Ponthalmazok, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1973/január: Pontversenyen kívüli P.164

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha a pontok egy egyenesen vannak, az állítás könnyen belátható. A következő megoldás azonban ebben az esetben nem működik, ezért ennek az esetnek a tisztázását az olvasóra hagyjuk.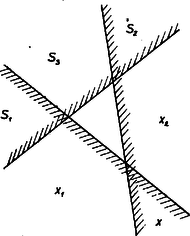
Kössük össze egyenessel a pontrendszerhez tartozó pontpárokat, és tekintsük az így kapott egyenesek által határolt félsíkokat. Nevezzünk egy ilyen félsíkot ,,telített''-nek, ha a pontoknak több mint (2/3)-a bennük van. Megmutatjuk, hogy a telített félsíkok metszete nem üres, és a metszet bármely pontja választható a feladatban szereplő P pontnak.
Tegyük fel az első állításunkkal ellentétben, hogy a telített félsíkoknak nincs közös pontjuk. Nevezzünk egy természetes k számot "elválasztó''-nak, ha található a telített félsíkok között k úgy, hogy ezek metszete már üres. Eszerint a telített félsíkok N száma elválasztó. Vegyük a legkisebb elválasztó számot, és jelöljük azt m-mel. Két esetet különböztetünk meg aszerint, hogy m egyenlő-e 3-mal vagy sem.
Ha m=3, akkor legyen S1, S2, S3 az a három telített félsík, amelyek metszete üres (1. ábra; ha több ilyen van, úgy az S1, S2, S3 hármas bármelyikük lehet).

 

 

1. ábra
 

Jelöljük az S1 és S2 közös részében levő pontok számát x-szel, a csak S1-ben levő pontokét x1-gyel, a csak S2-ben levőkét x2-vel. Feltevéseink szerint egyrészt
x+x1>23nésx+x2>23n
másrészt
x+x1+x2≦n,
tehát x>13n. Hasonlóan kapjuk, hogy S2 és S3, valamint S3 és S1 metszetében is 13n-nél több pont van, ami nyilvánvaló ellentmondás.
Rátérünk az m>3 eset vizsgálatára. Legyenek S1,S2,...,Sm azok a telített félsíkok, amelyek metszete üres (ha több lehetőség van a választásra, ismét tetszőlegesen választhatunk). Mivel m a legkisebb elválasztó szám, akárhogy hagyunk el egyet e síkok közül, a többiek metszete már nem lehet üres. Legyen Pi olyan pont, amelyik Si kivételével mindegyik mondott félsíkban benne van (i=1,2,...,m). Tekintsük a P1, P2, P3, P4 pontok konvex burkát: ha ez egy szakasz vagy háromszög, legyen Q a P1, P2, P3, P4 pontok közül az, amelyik nem csúcsa (vagy végpontja) a konvex buroknak, ha pedig négyszög, akkor Q legyen az átlók metszéspontja. Könnyű ellenőrizni, hogy ez a Q az Si síkok mindegyikében benne van, tehát ismét ellentmondásra jutottunk.
Ezzel beláttuk, hogy van olyan P pont, amelyik mindegyik telített félsíkban benne van. Azt kell még megmutatnunk, hogy minden P-n átmenő egyenes mindkét partján legalább n/3 pont található. Ismét tegyük fel, hogy ez nem igaz, és legyen e olyan P-n átmenő egyenes, amelynek egyik oldalán (az F1 félsíkban) (n/3)-nál kevesebb pont van (2. ábra).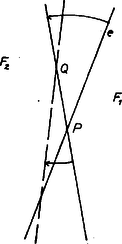
 

 

1. ábra
 

Akkor e-nek a másik oldalán (az F2 félsíkban) ‐ az e-n levő pontokat nem is számítva ‐ több mint 23n pont van.
Ha van e-n az adott pontok közül való, legyen Q köztük a P-től legtávolabbi (ha két ilyen pont is volna, ezek egyike). Ha ilyen pont nincs, forgassuk e-t P körül pozitív forgásirányba mindaddig, amíg az adott pontok valamelyikébe nem ütközik. Ha ebben a helyzetben van rajta F2-beli adott pont, Q legyen ezek közül a P-hez legközelebbi; ha ilyen nincs, Q legyen a P-től legtávolabb levő, az egyenesen levő adott pont.
Forgassuk tovább e-t Q körül olyan irányban, hogy e új helyzetében P és az F1-beli adott pontok e-nek ugyanazon az oldalán legyenek. Tartson ez a forgatás mindaddig, amíg a pontrendszer újabb pontjába nem ütközik. Mivel a pontok nem az egyenes pontjai, ez hamarabb bekövetkezik, mint hogy kiinduló helyzetünkbe visszatérünk. Forgatás közben egyetlen adott pont sem került át e egyik oldaláról a másikra, e-nek tehát a P-t nem tartalmazó oldala telített félsík, amelyikben P nincs benne. Ismét ellentmondásra jutottunk, ezzel az előrebocsátottak értelmében a feladat megoldását befejeztük.