Feladat: Pontversenyen kívüli P.163 Korcsoport: - Nehézségi fok: -
Füzet: 1975/május, 212 - 214. oldal  PDF  |  MathML 
Témakör(ök): Poliéderek súlypontja, Térgeometriai bizonyítások, Tetraéderek, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1973/január: Pontversenyen kívüli P.163

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen P a tetraéder tetszőleges belső pontja, és mondjuk azt, hogy a tetraéder valamelyik lapja P-re nézve labilis, ha P-nek az illető lap síkján levő merőleges vetülete kívül van a testen. Megmutatjuk, hogy ha P-re egy bizonyos feltétel teljesül, akkor a tetraédernek legfeljebb két, a P-re nézve labilis lapja lehet. Ez a bizonyos feltétel olyan lesz, hogy az a súlypontra mindig teljesül; ezzel tehát belátjuk a feladat állítását. ‐ Itt nem fogjuk megvizsgálni, hogy elképzelhető-e olyan tetraéder, melynek van olyan ‐ a súlyponttól különböző ‐ belső pontja, melyre ez a feltétel nem teljesül, csak megjegyezzük, hogy ilyen példa megadható.
Legyen tehát P egy adott pont a tetraéder belsejében, melynek egy bizonyos később tisztázandó tulajdonsága megvan. Ha a tetraéder valamelyik lapja P-re nézve labilis, P-től az illető lap felé a P-ből a lapra bocsátott merőleges mentén haladva előbb lépünk ki a tetraéderből, mintsem az illető lapot elérnénk, a merőleges egyenes előbb a tetraéder valamelyik másik lapját metszi. Mondjuk azt, hogy ez a másik lap P-ből nézve takarja az illető, P-re nézve labilis lapot.
Az ilyen, labilis lapokat takaró lapok mindig közelebb vannak P-hez, mint maga a labilis lap, hiszen már a labilis lapra merőleges egyenes mentén van a P-hez közelebbi pontjuk. Emiatt a P-hez legközelebbi lap nem lehet P-re nézve labilis, a többi lap ugyanis nem tudja takarni. Egy nem labilis lap ‐ nevezzük az ilyet stabilnak ‐ tehát tetszőleges P-re nézve létezik.
Jelöljük ennek a lapnak a síkját S1-gyel, P-nek S1-en levő vetületét P1-gyel. A PP1 egyenes még egy pontban metszi a tetraéder felületét, jelöljük ezt Q-val, és az átmetszett lap síkját S2-vel. Ha S2 stabil, akkor már csak a még nem említett lapok lehetnek labilisak, állításunk tehát igaz.
Előfordulhat azonban, hogy S2 labilis. Jelöljük ekkor az S2-t takaró lap síkját S3-mal, a negyedik lapsíkot S4-gyel, és vizsgáljuk meg, mi a feltétele annak, hogy S3 stabilis legyen. S3-at S2 nyilván nem takarhatja, hiszen S3 közelebb van P-hez, mint S2. Megmutatjuk, hogy S3-at S4 sem takarhatja, és ha P nincs túl közel S1-hez, pontosabban mondva, ha

PP1>2-12⋅PQ,(1)
akkor S1 sem takarhatja S3-at. Ha tehát P-re teljesül (1), akkor vagy már S2 stabilis, vagy ha ez nem is az, akkor S3 biztosan az. ‐ Amennyiben P a tetraéder súlypontja, akkor (1) teljesül, hiszen ekkor
PP1PQ≥13>2-12=0,207.

Jelöljük a tetraéder Si-vel szemközti csúcsát Ai-vel, P-nek Si-n levő vetületét Pi-vel (i=1,2,3,4). A P2 pontból a PQ szakasz derékszög alatt látszik, P2 tehát rajta van a PQ feletti Thalész-gömbön. Ha S3 takarja S2-t, azaz P2 az S3 síknak a tetraéderrel ellentétes oldalán van, akkor a PP3P2 szög tompaszög, tehát P3 a PP2 szakasz feletti Thalész-gömb belső pontja. Megmutatható, hogy ha adott egy G gömb, a G húrjai feletti Thalész-gömbök egyesítése egy, a G-vel koncentrikus gömböt tölt ki, amelynek a sugara G sugarának a 2-szerese. Ha, P-re teljesül (1), a PQ feletti Thalész-gömböt a centrumából 2-szeresére növelve, még mindig teljes egészében S1 felett marad, ekkor tehát P3 az S1-nek ugyanazon az oldalán van, mint maga a tetraéder, vagyis S1 nem takarhatja S3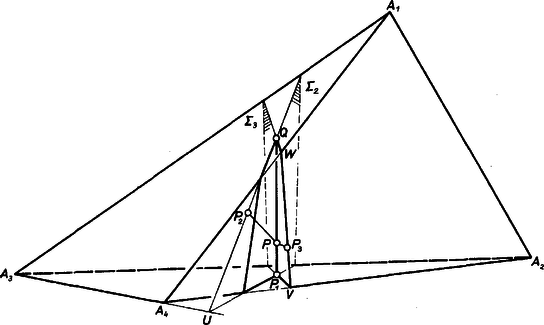-at.
 

 

Meg kell még mutatnunk, hogy ha S3 takarja S2-t, akkor S4 nem takarhatja S3-at. Jelöljük a PQ-n átmenő, Si-re merőleges síkot Σi-vel (i=2,3). Σ2 merőleges S1-re, tehát A3A4-re is, így mindenesetre metszi azt, jelöljük a metszéspontot U-val. A P1QU háromszögben P1-nél derékszög van, emiatt a P1Q szakaszon levő P pont vetülete a QU szakaszon van. Ez a vetület nem más, mint P2, hiszen Σ2⊥S2. Ha S3 takarja S2-t, P2 az S3-nak már a tetraédert nem tartalmazó oldalán van, és így ott van U is, tehát U az A3A4 szakasz A4-en túli meghosszabbításán van. Emiatt az A2A3A4 háromszögben A4-nél tompaszög van, és mivel P1U⊥A3A4, azért P1-nek az A2A4 egyenesen levő vetülete az A2A4 szakaszon is rajta van, jelöljük ezt V-vel. Az is az A2A3A4 háromszög és a P pont most megismert helyzetéből következik, hogy a P1V egyenes az A2A3 szakaszt is metszi, Σ3 tehát elválasztja A2-t az A3, A4 pontoktól. El kell választania Σ3-nak A1-et is az A3, A4 pontoktól, különben nem tartalmazhatná az A1A3A4 háromszög Q pontját. Σ3 tehát metszi az A1A4 szakaszt, jelöljük ezt a metszéspontot W-vel.
Tekintsük a QP1VW négyszöget. Mivel ebben P1-nél derékszög van, P3 a P1Q egyenesnek ugyanazon oldalán van, mint maga a négyszög. Ha tehát P-ből P3 felé haladva ki is lépünk a négyszögből, ezt csak a P1V, vagy QW szakaszon át tehetjük, ami épp azt jelenti, hogy S3 elé csak S1 vagy S2 állhat, de S4 semmi esetre sem. ‐ A bizonyítást ezzel befejeztük.